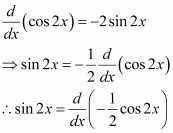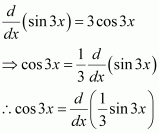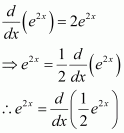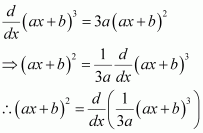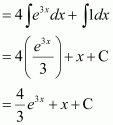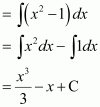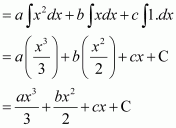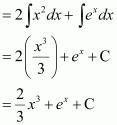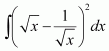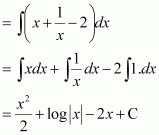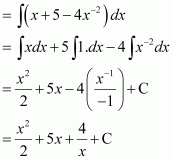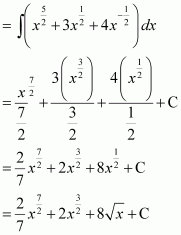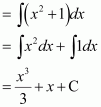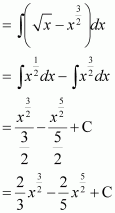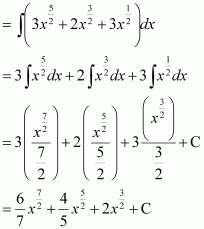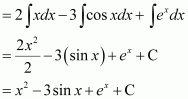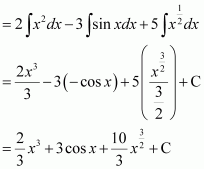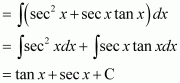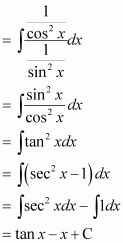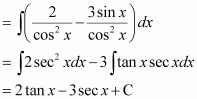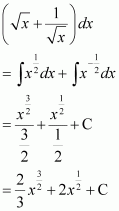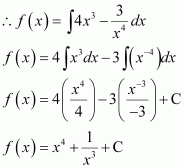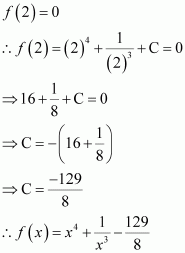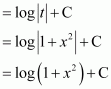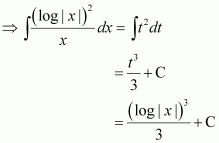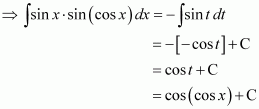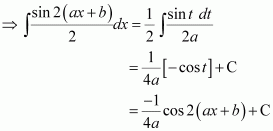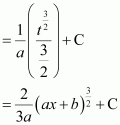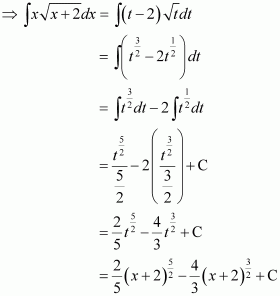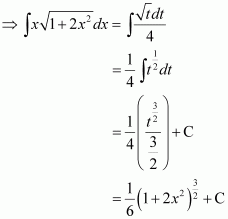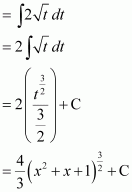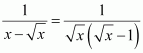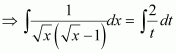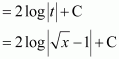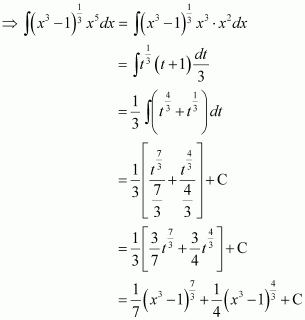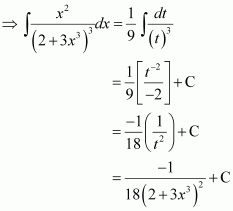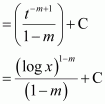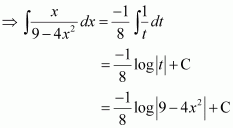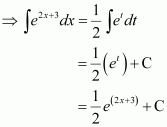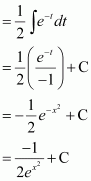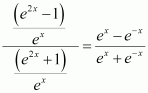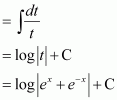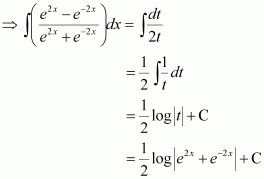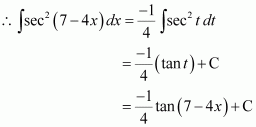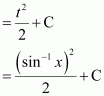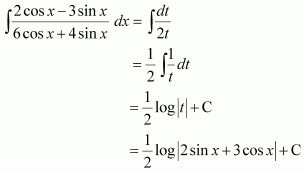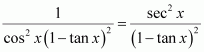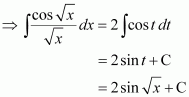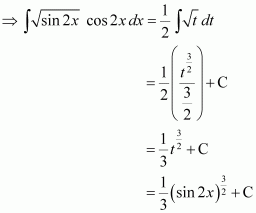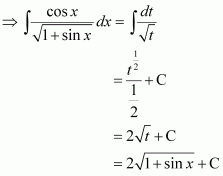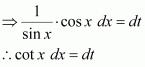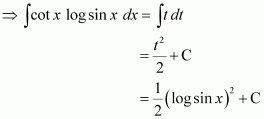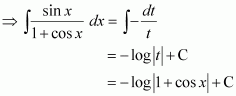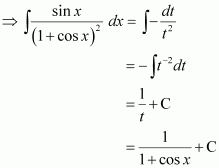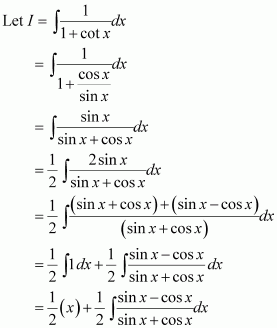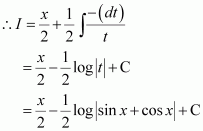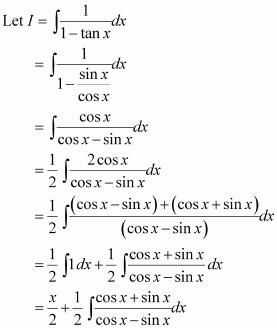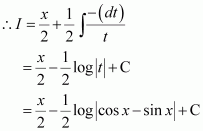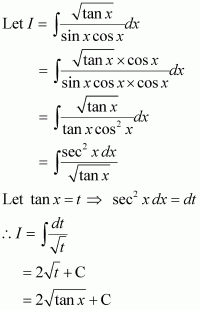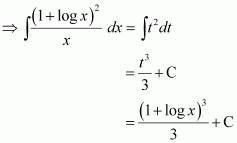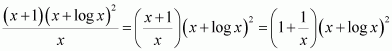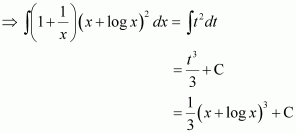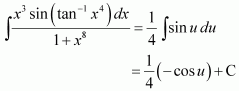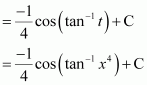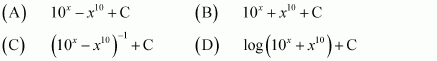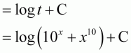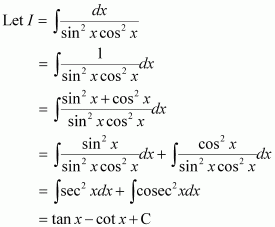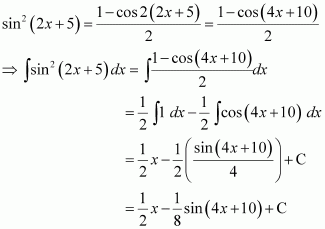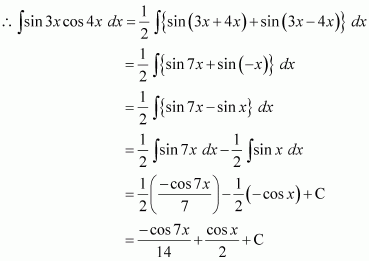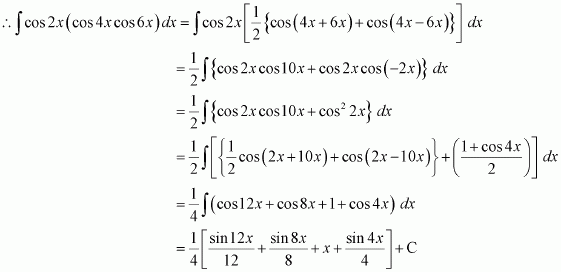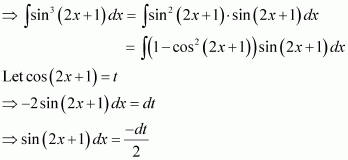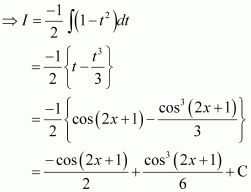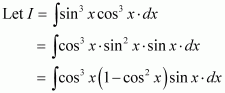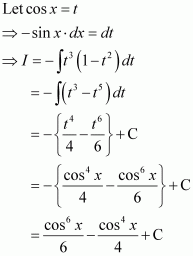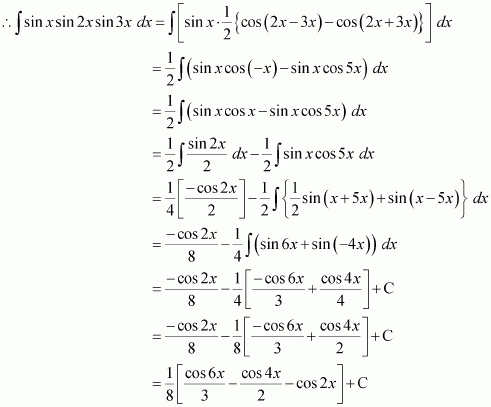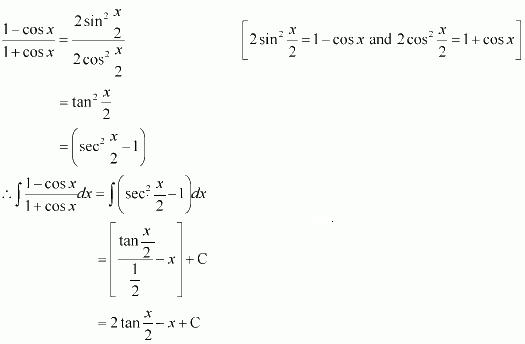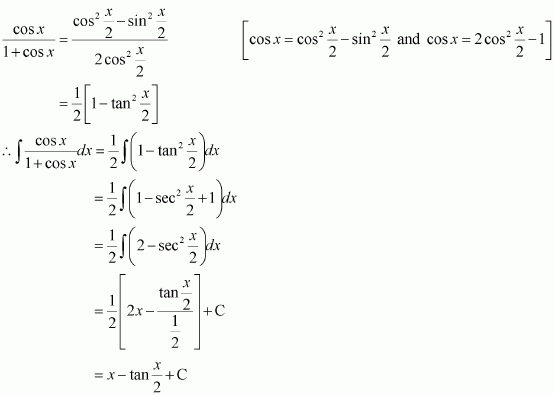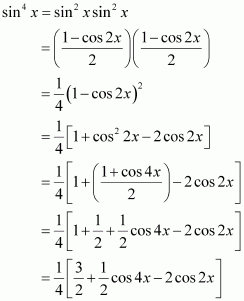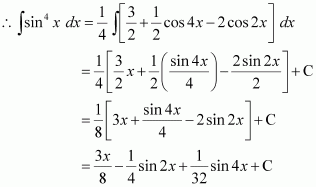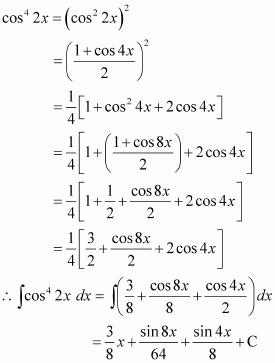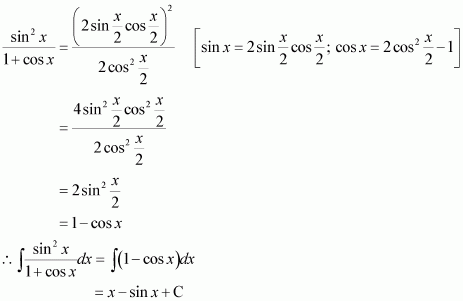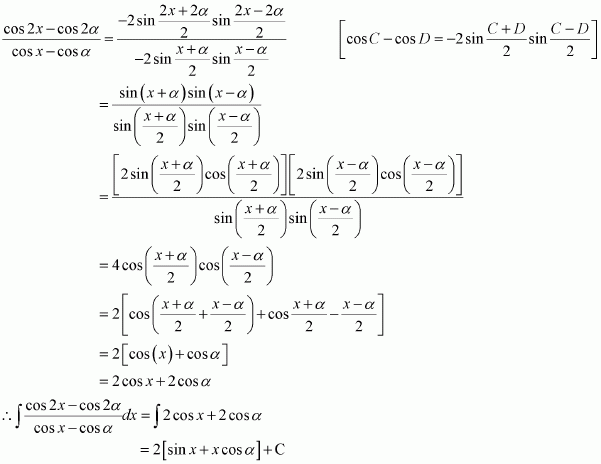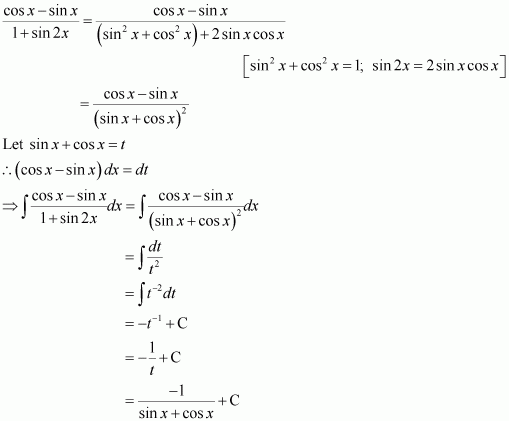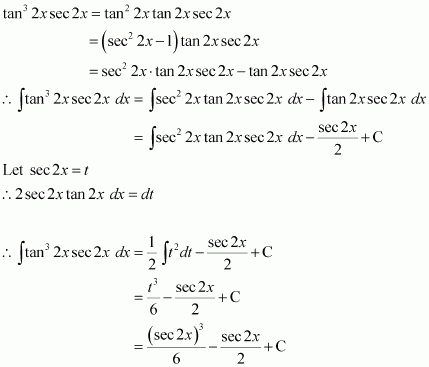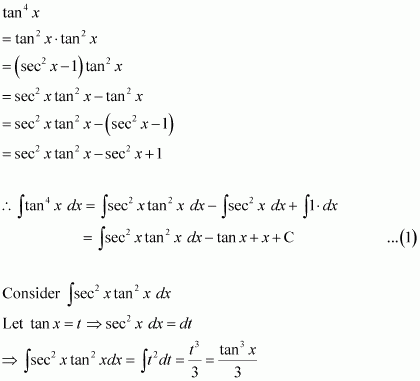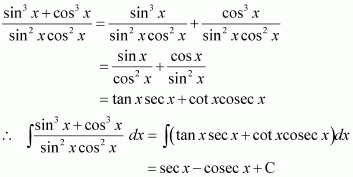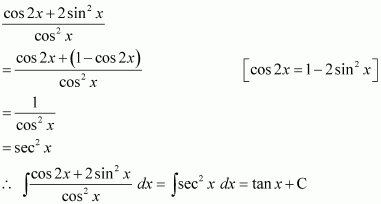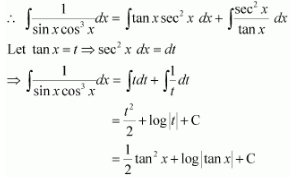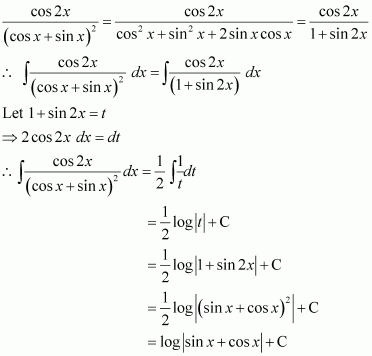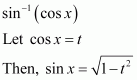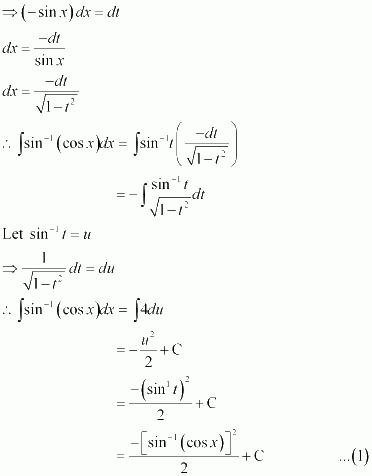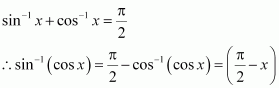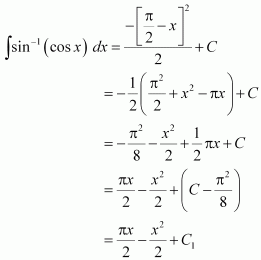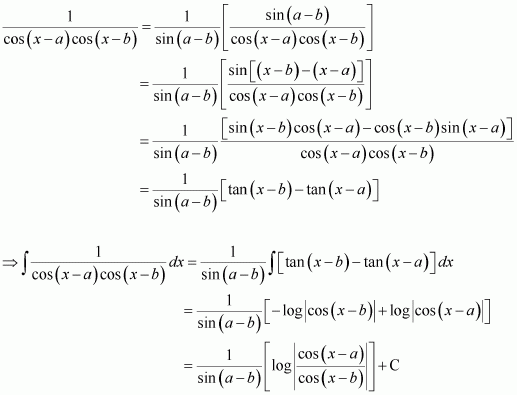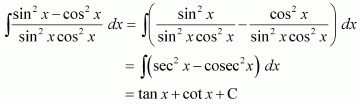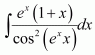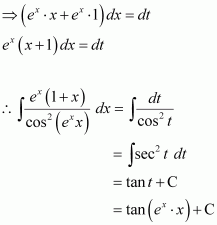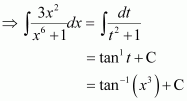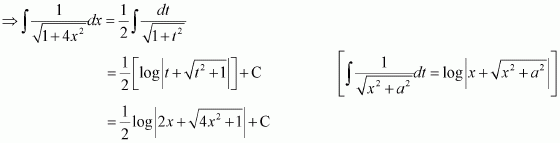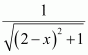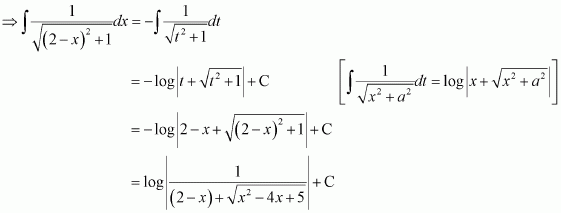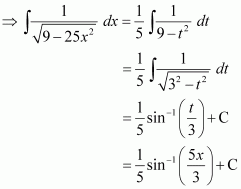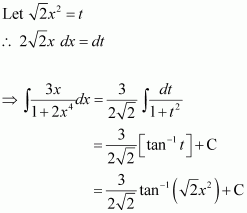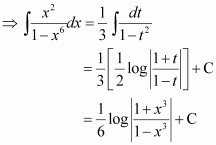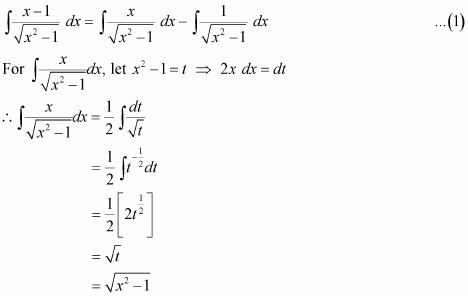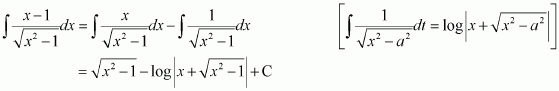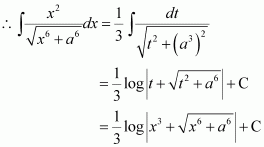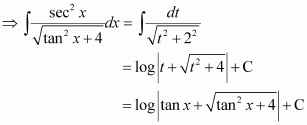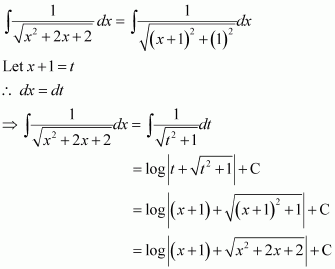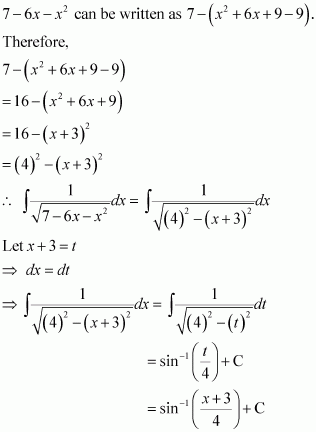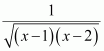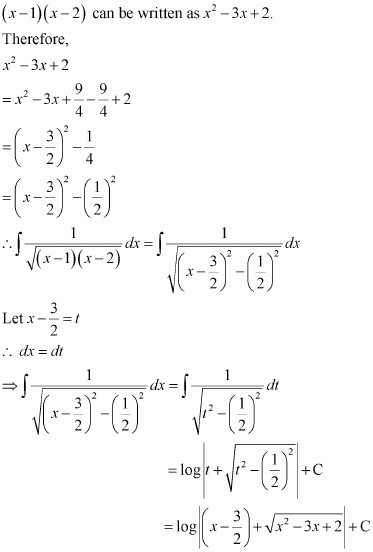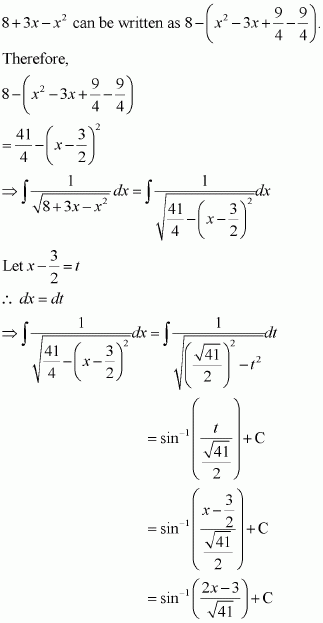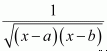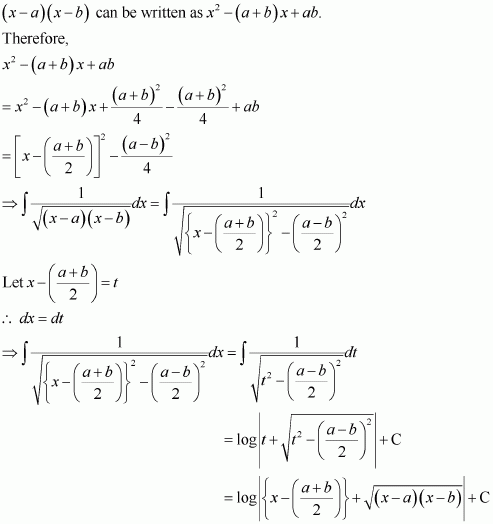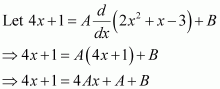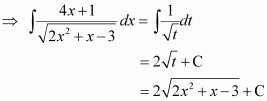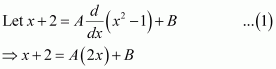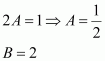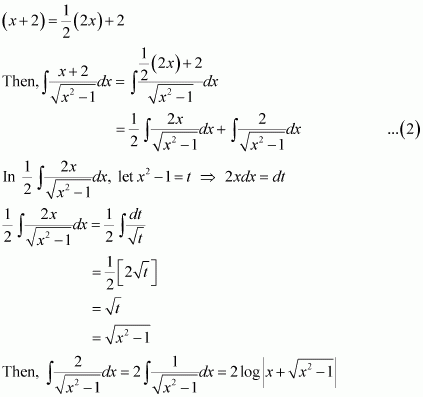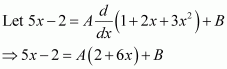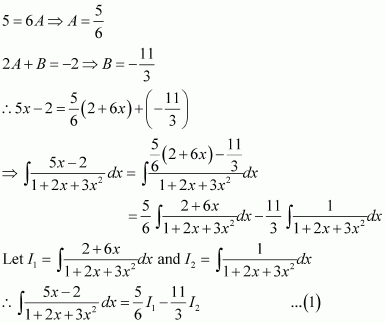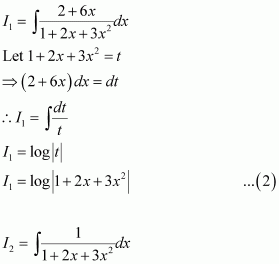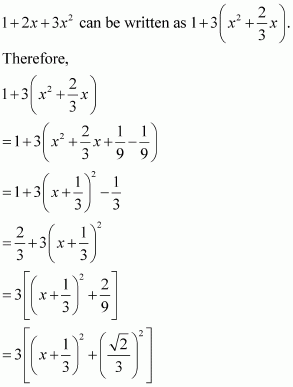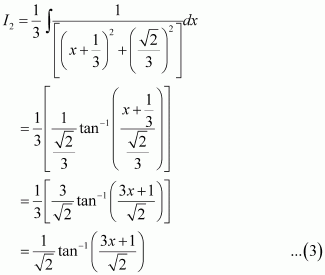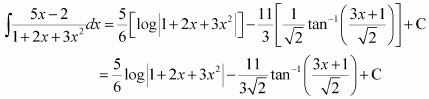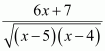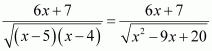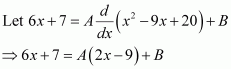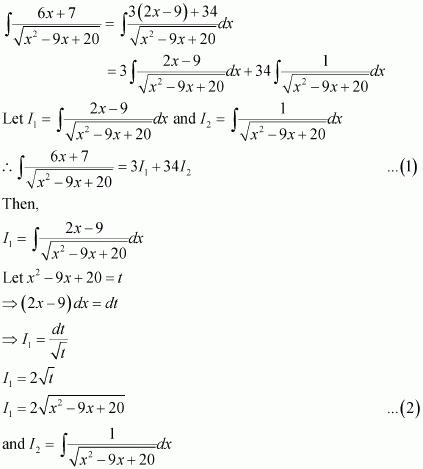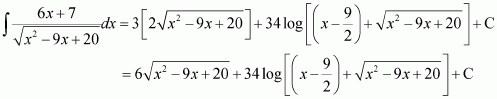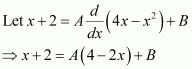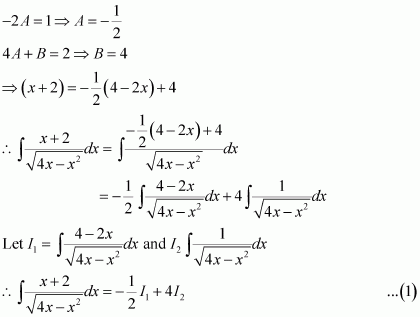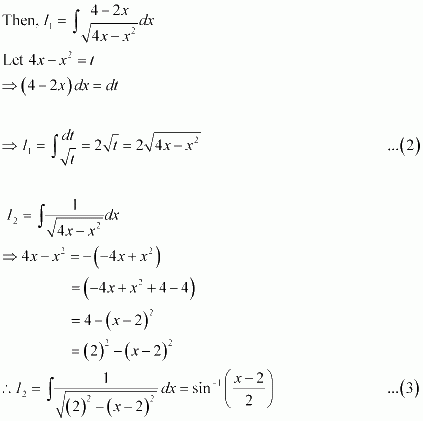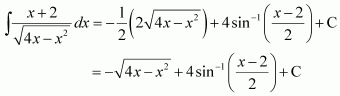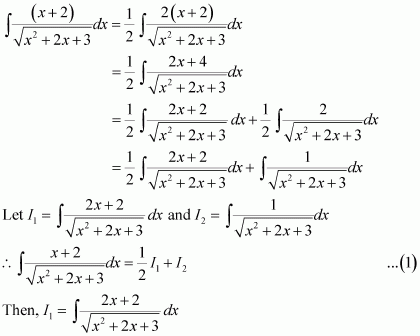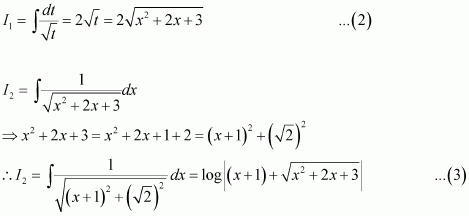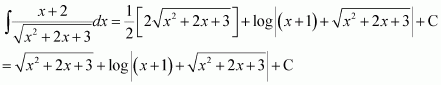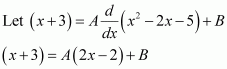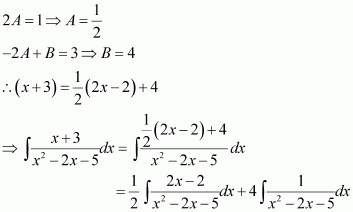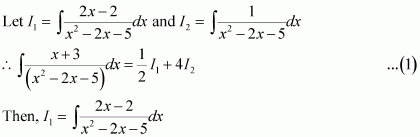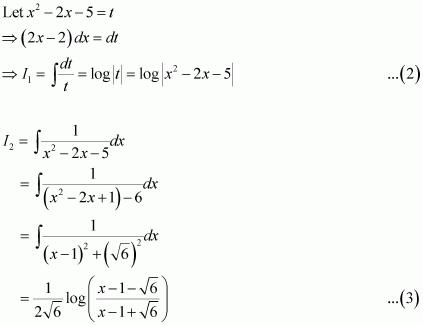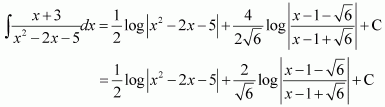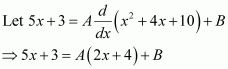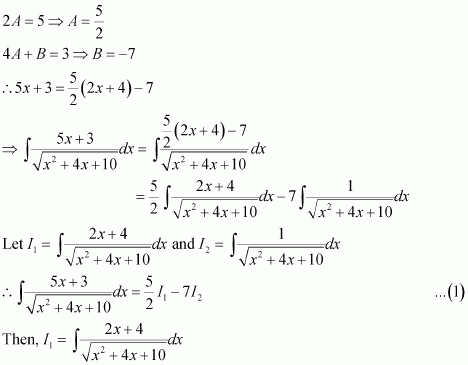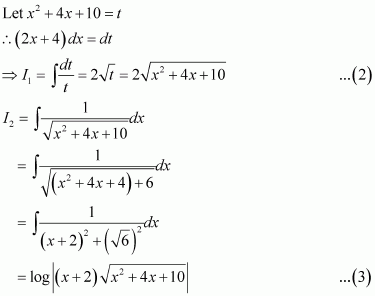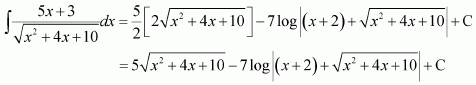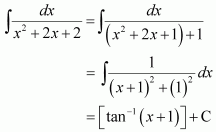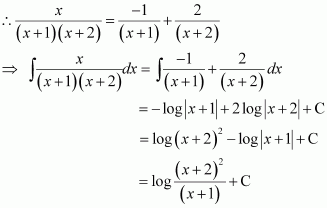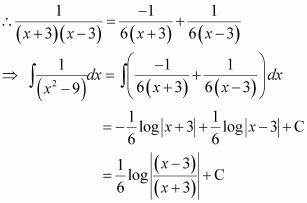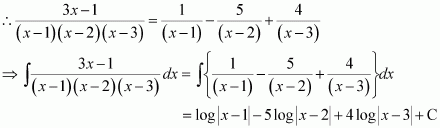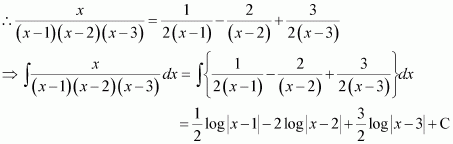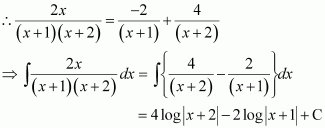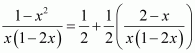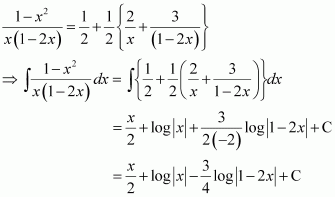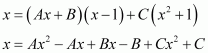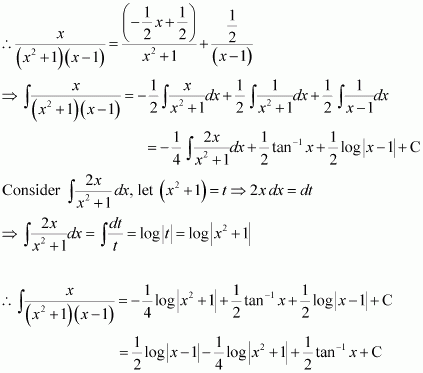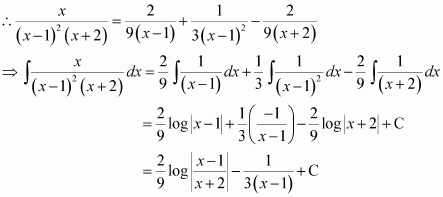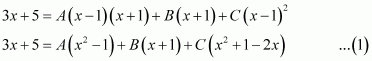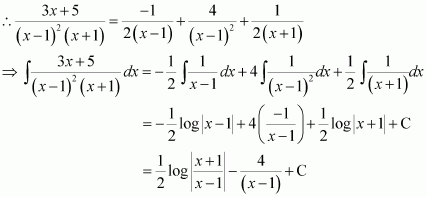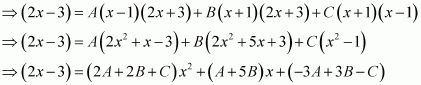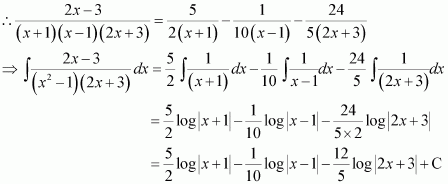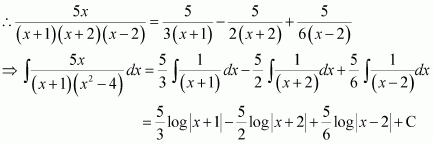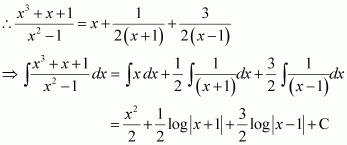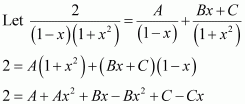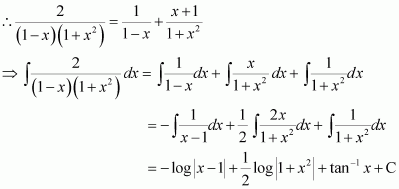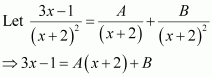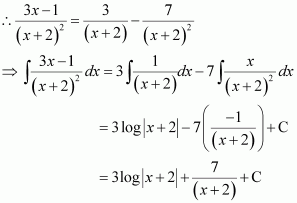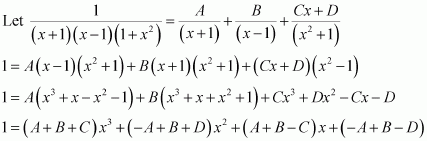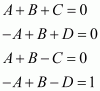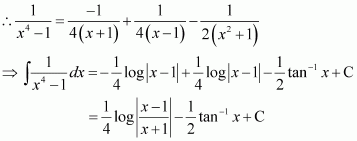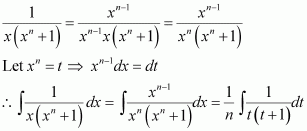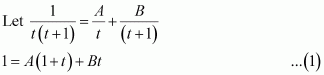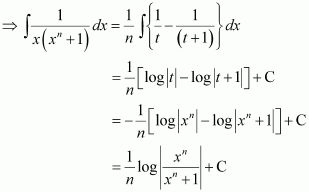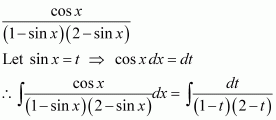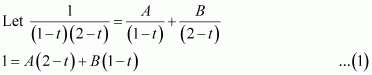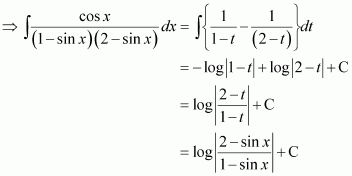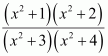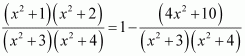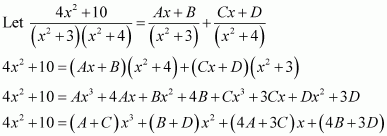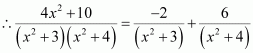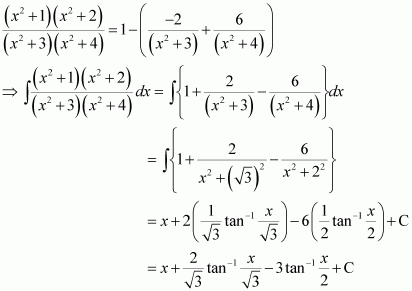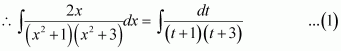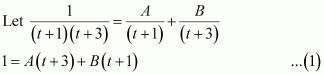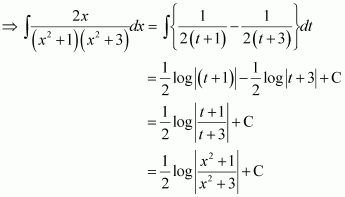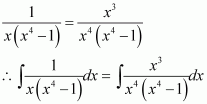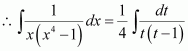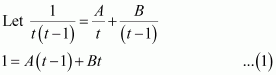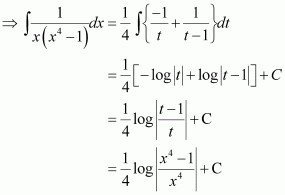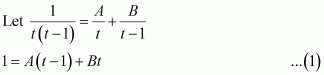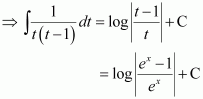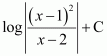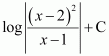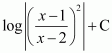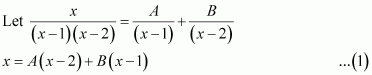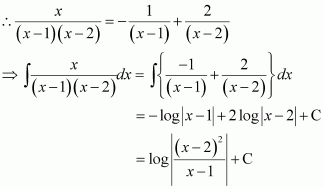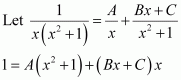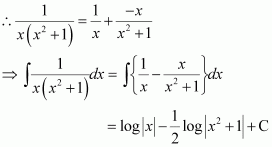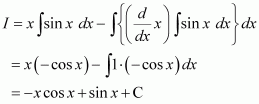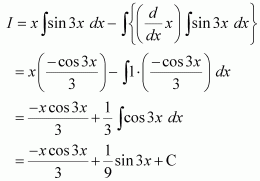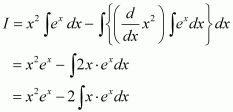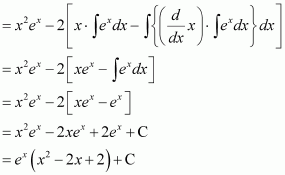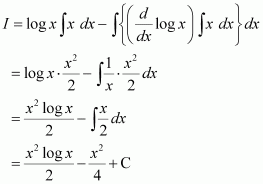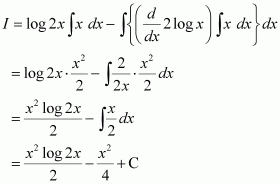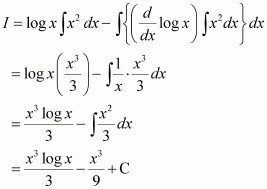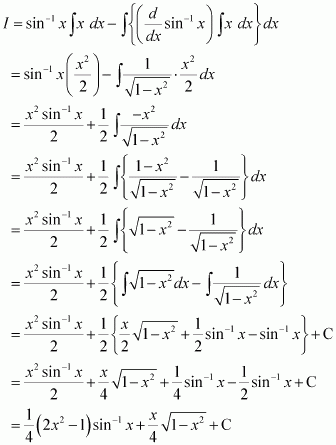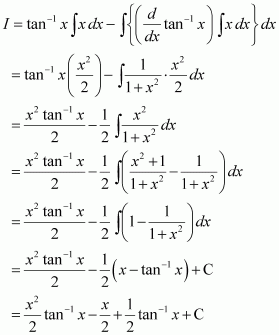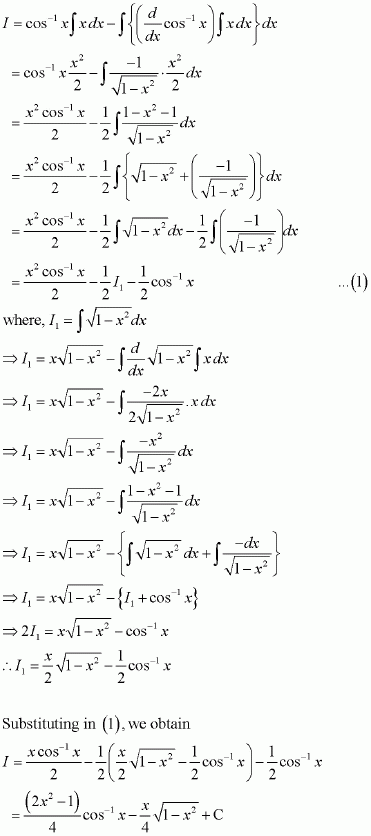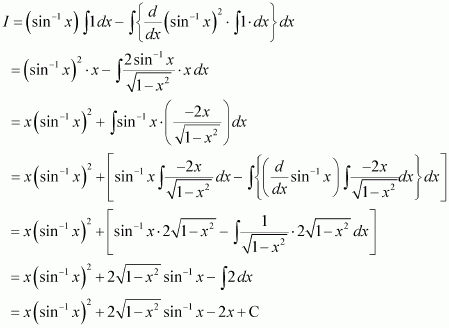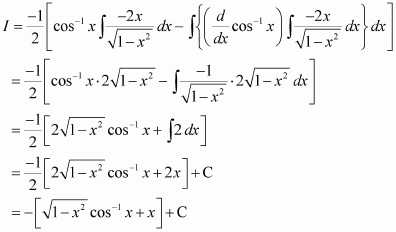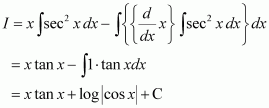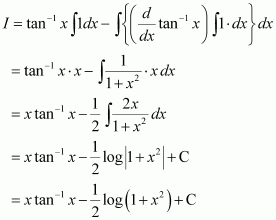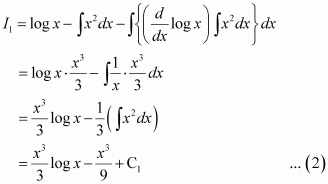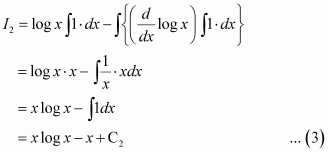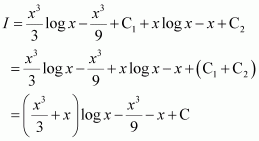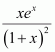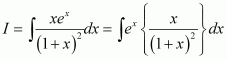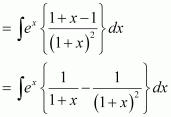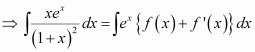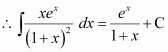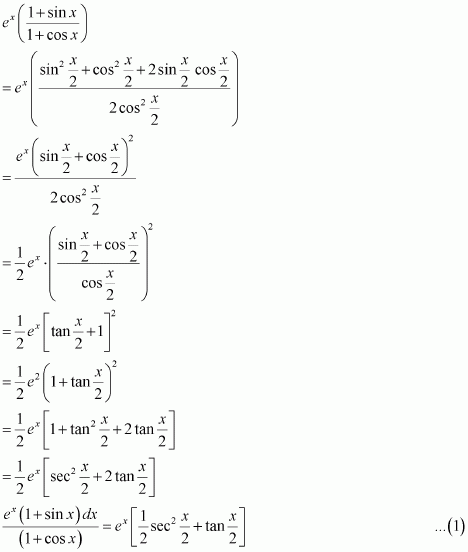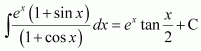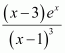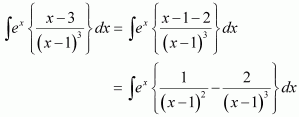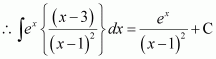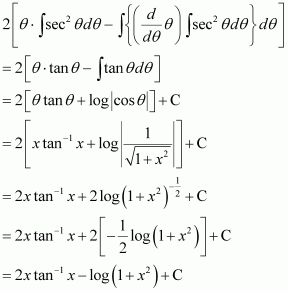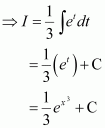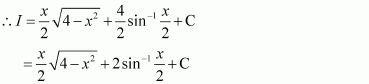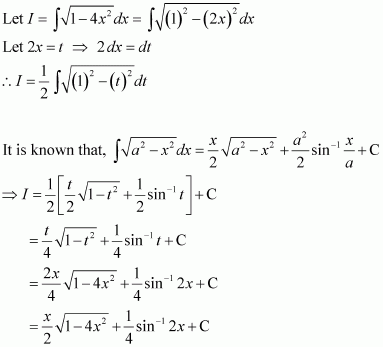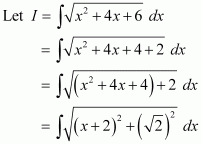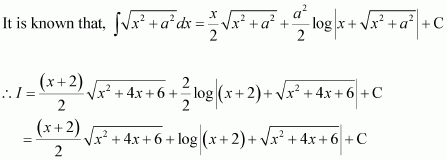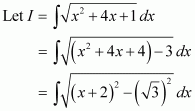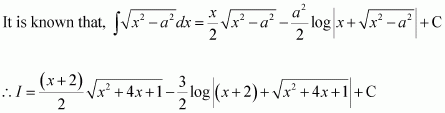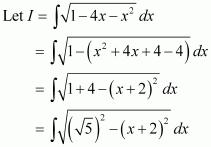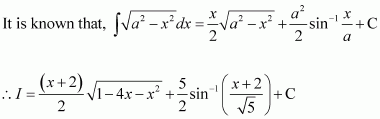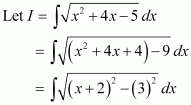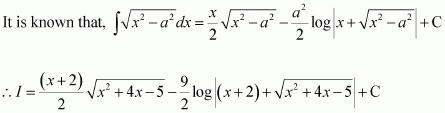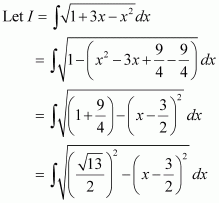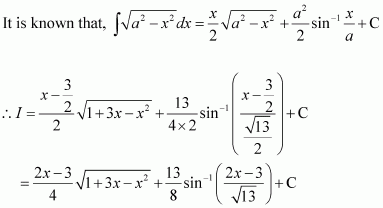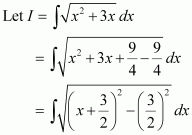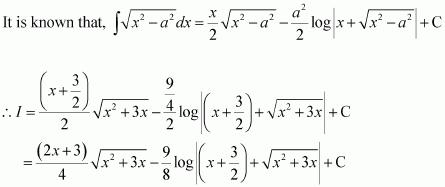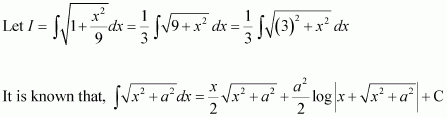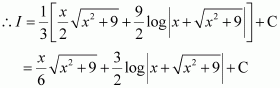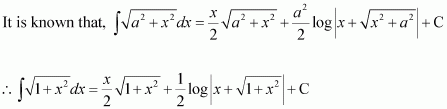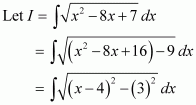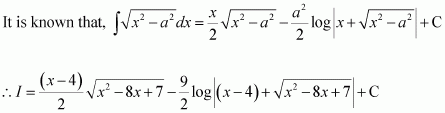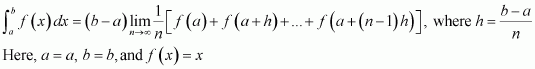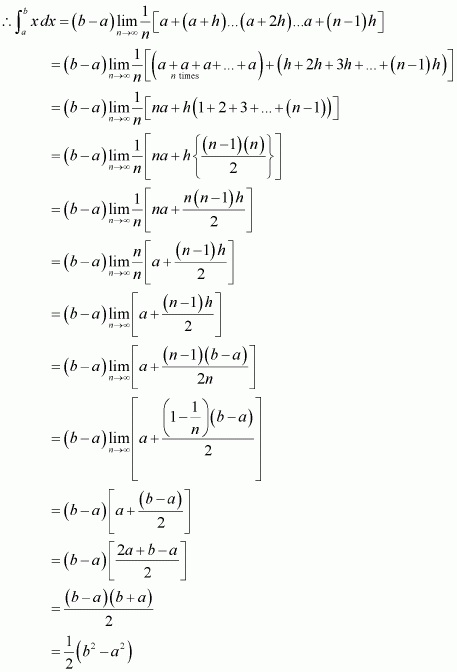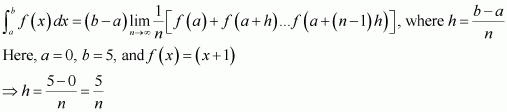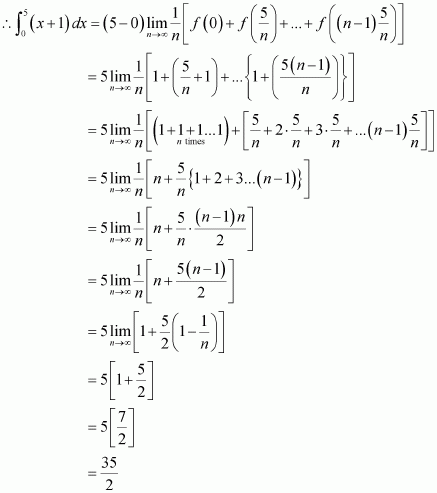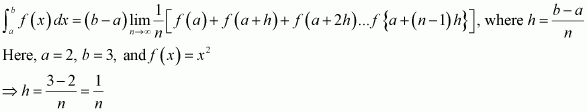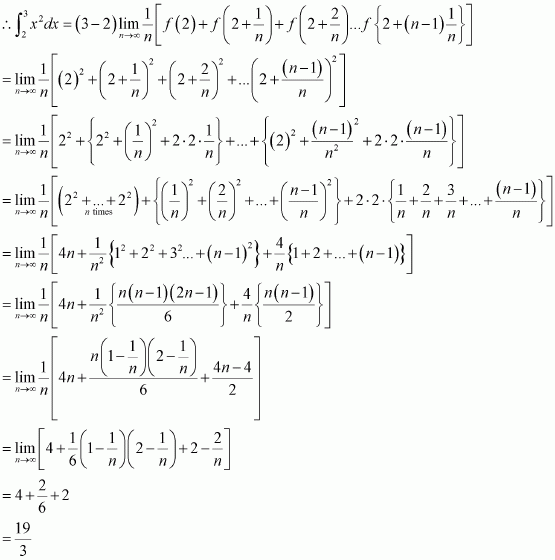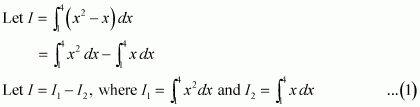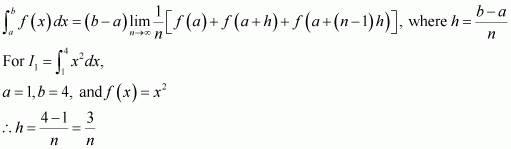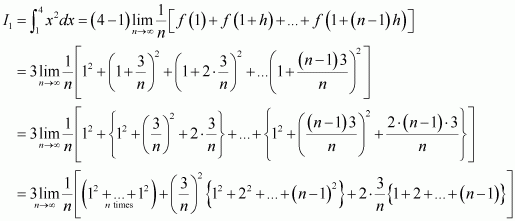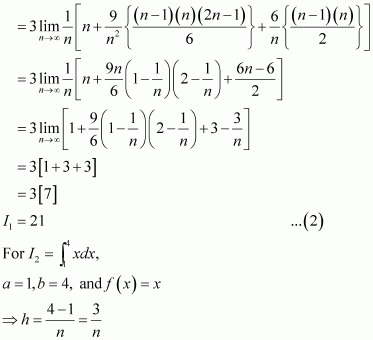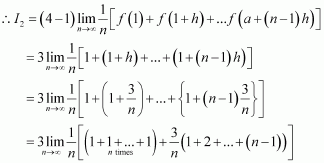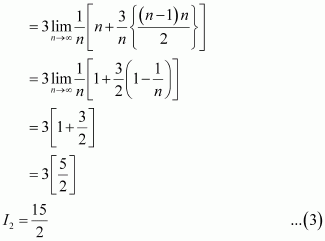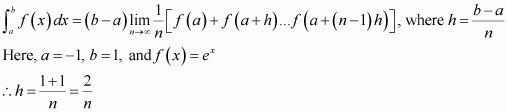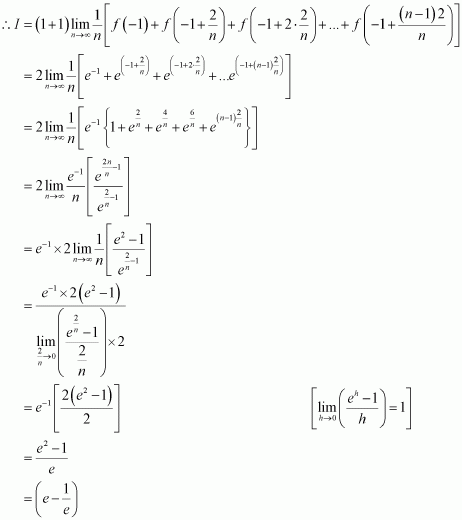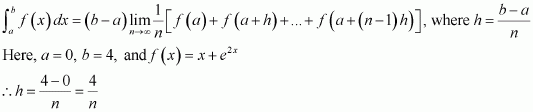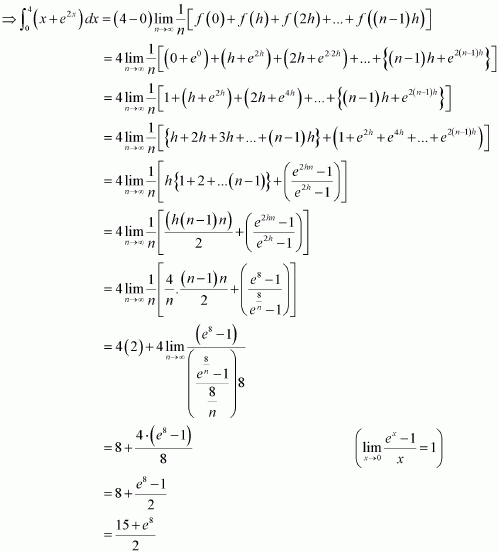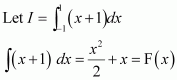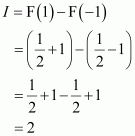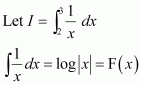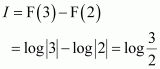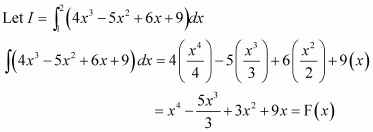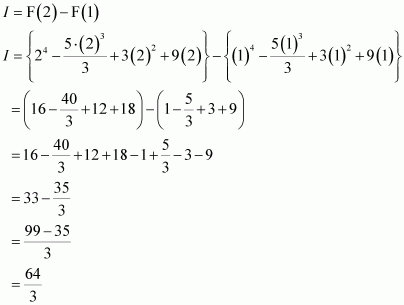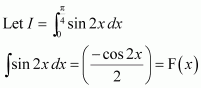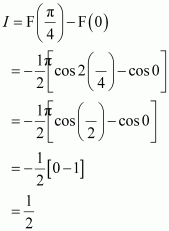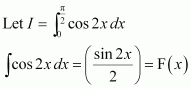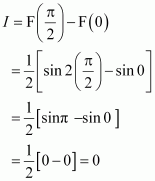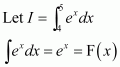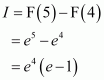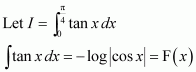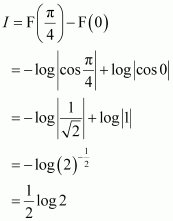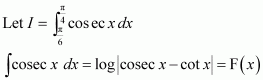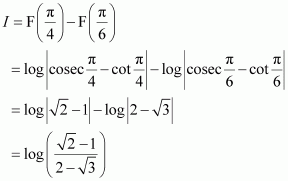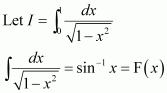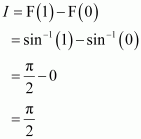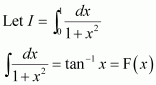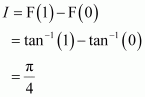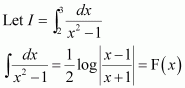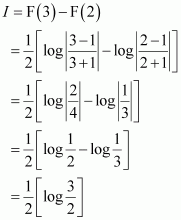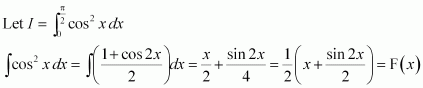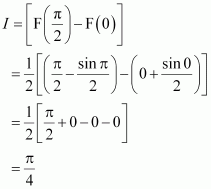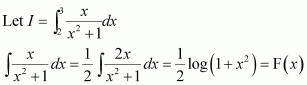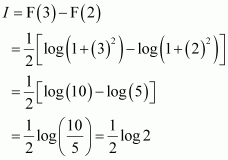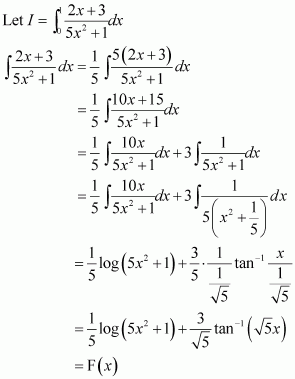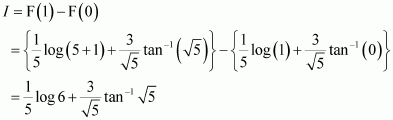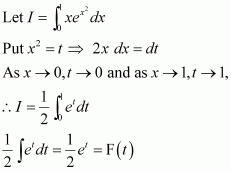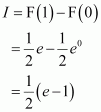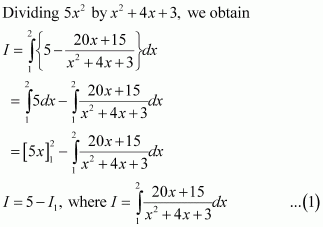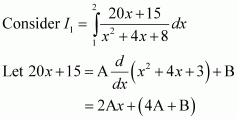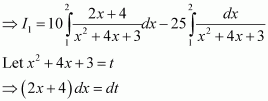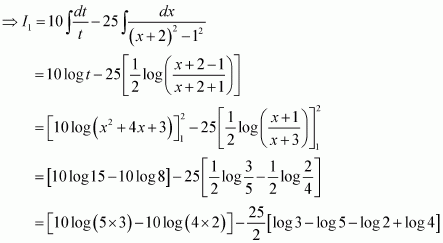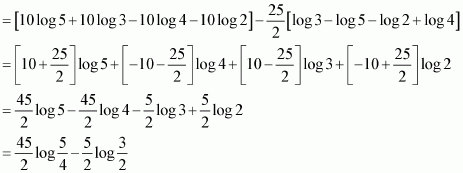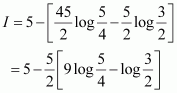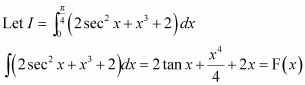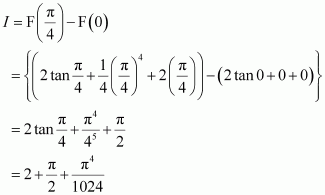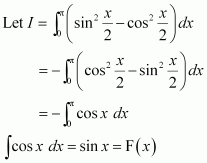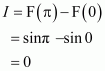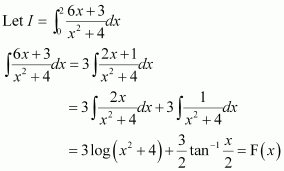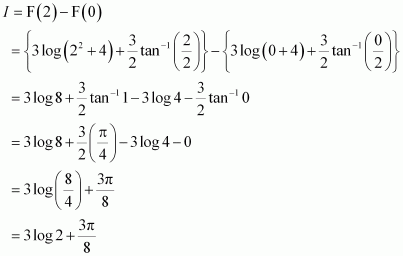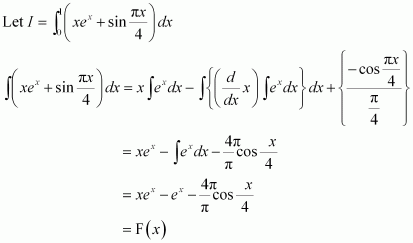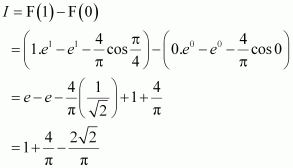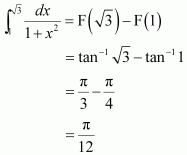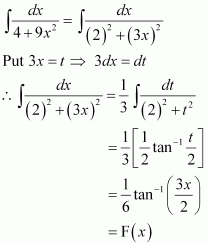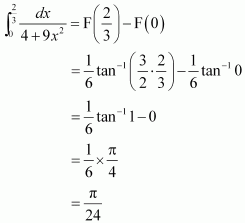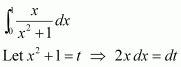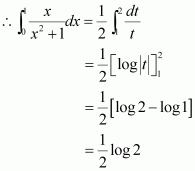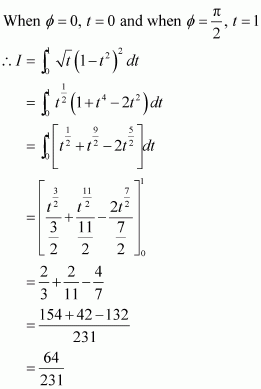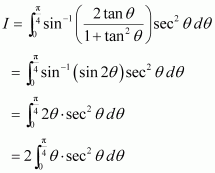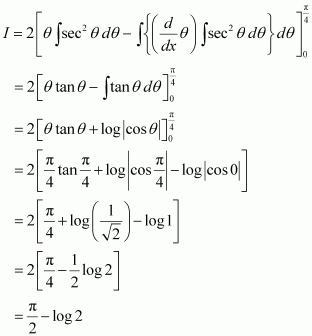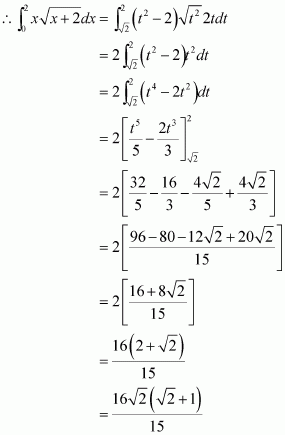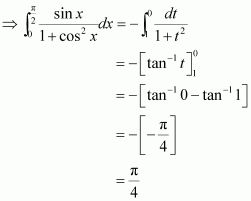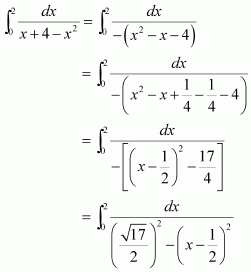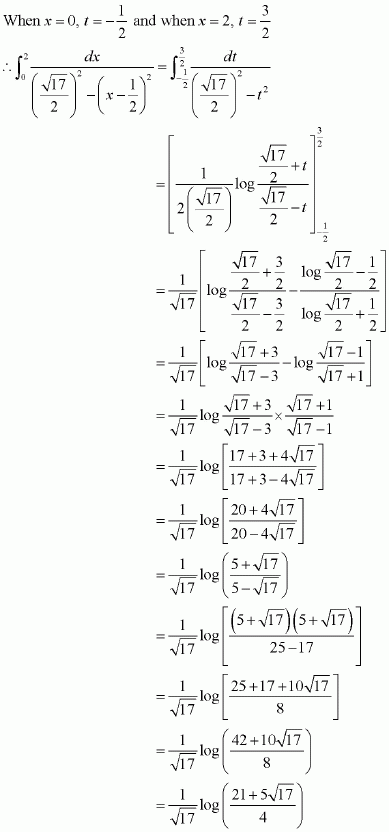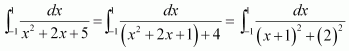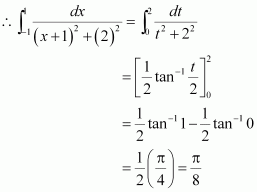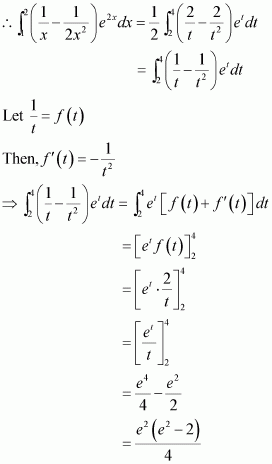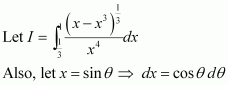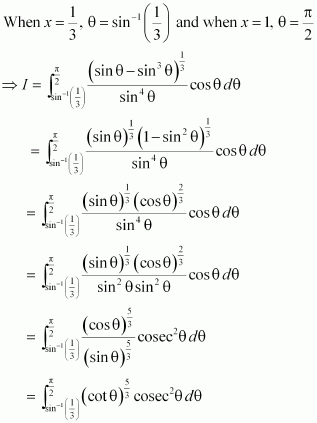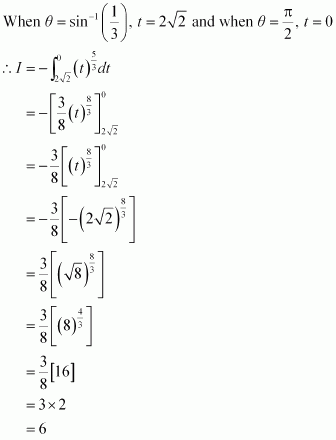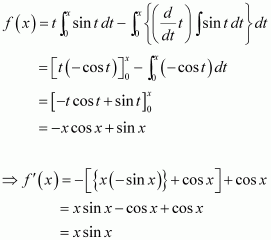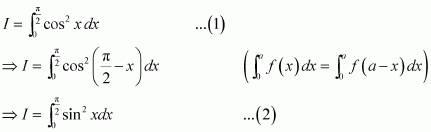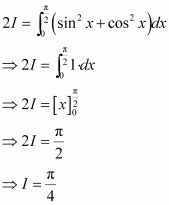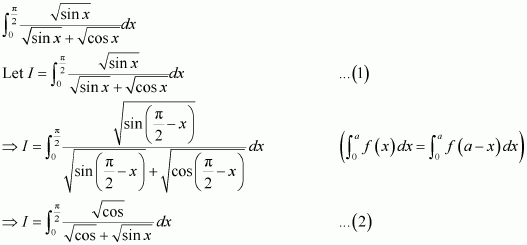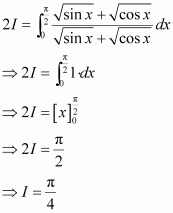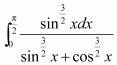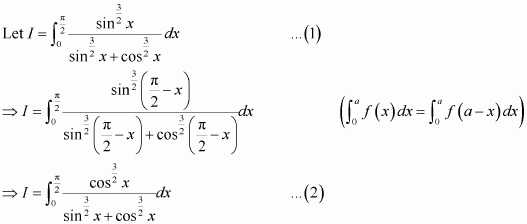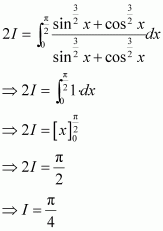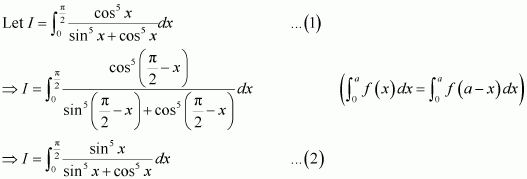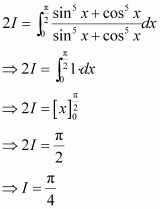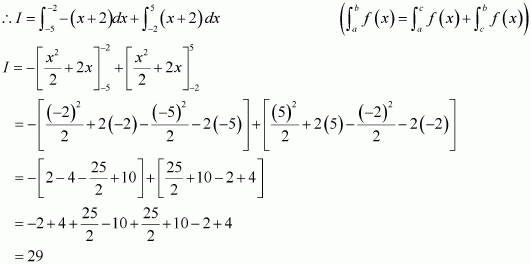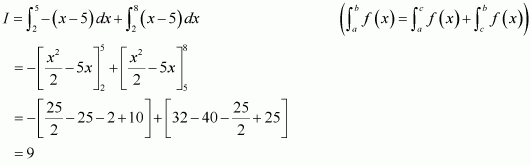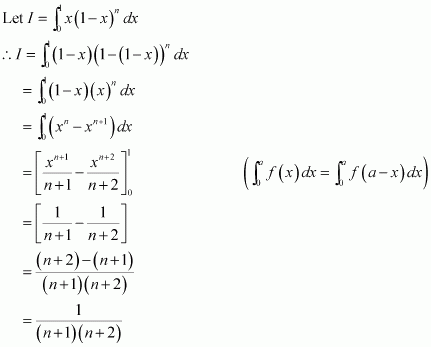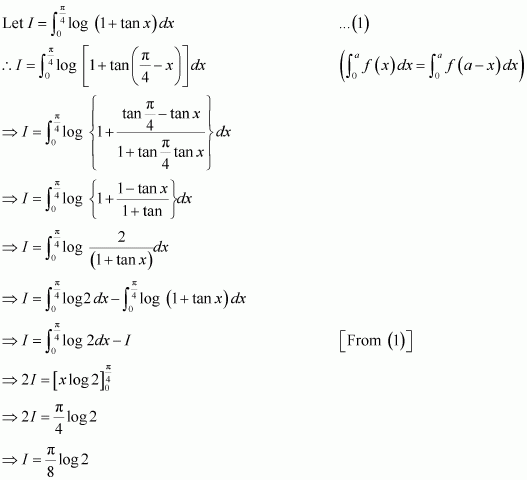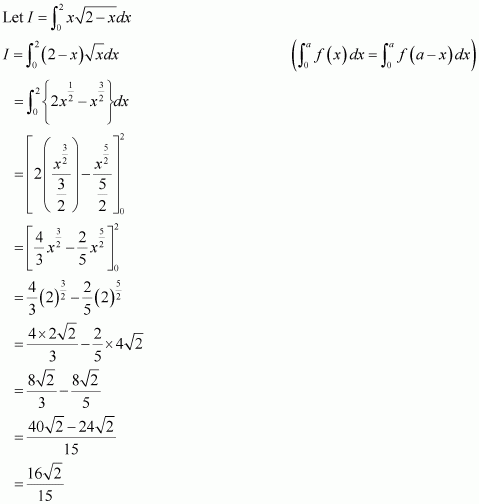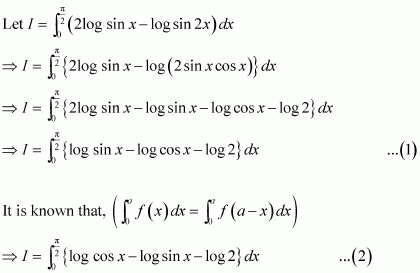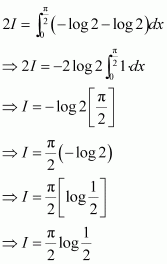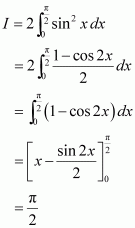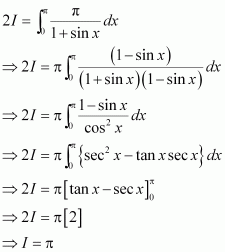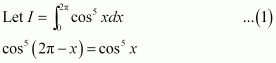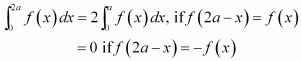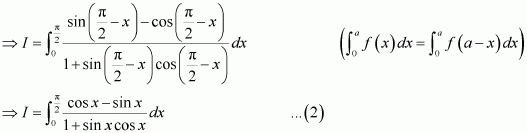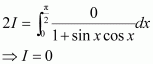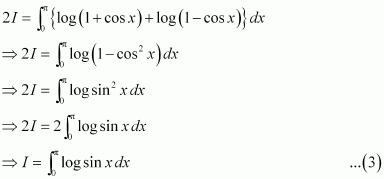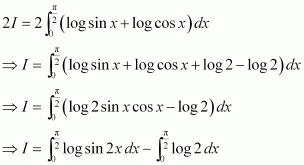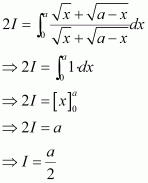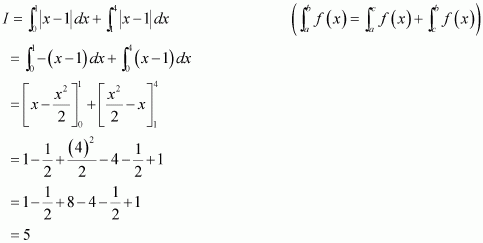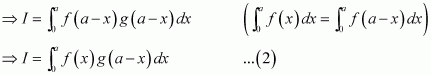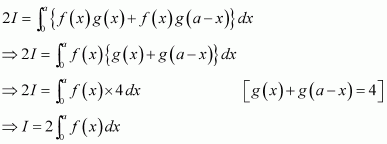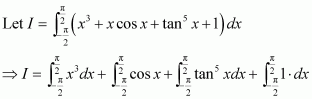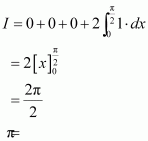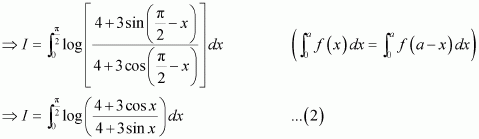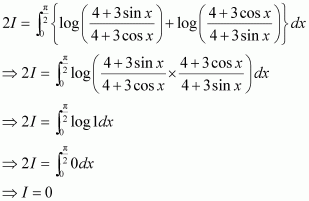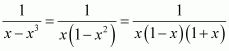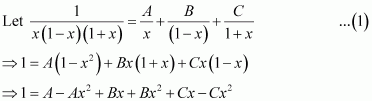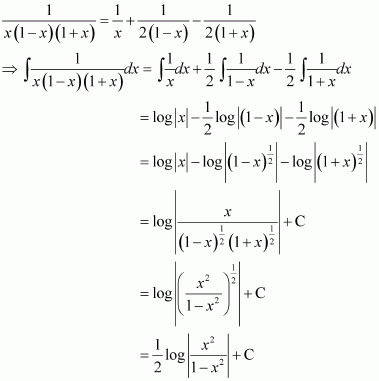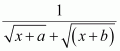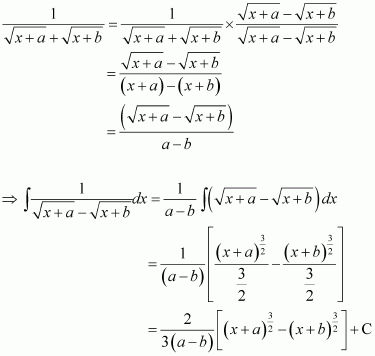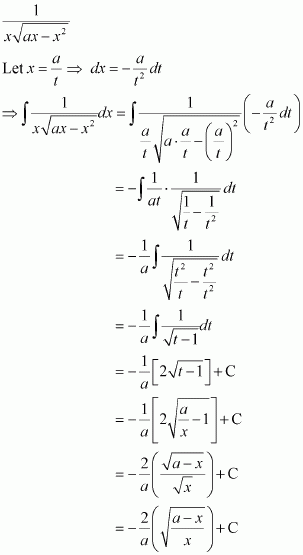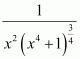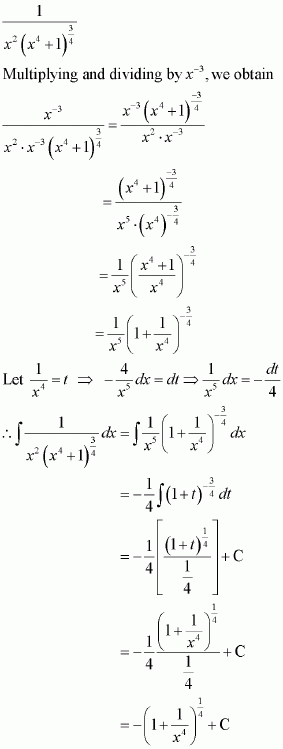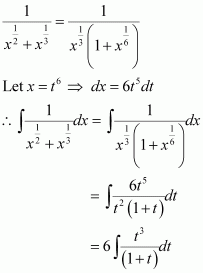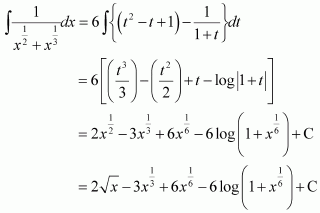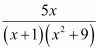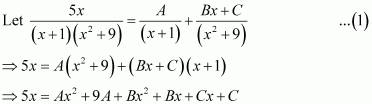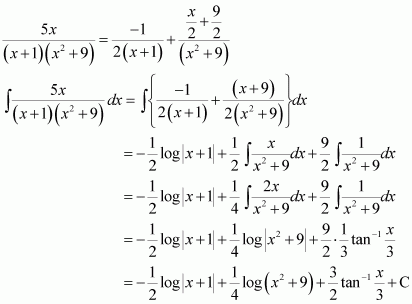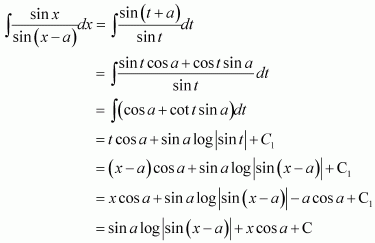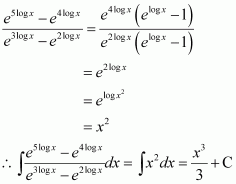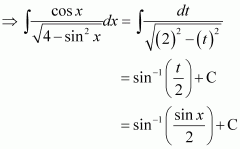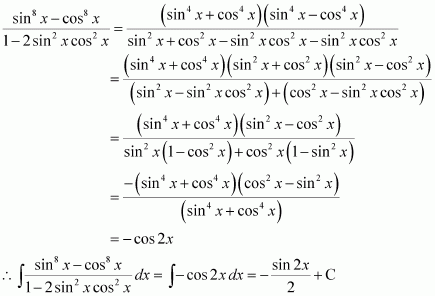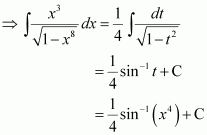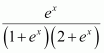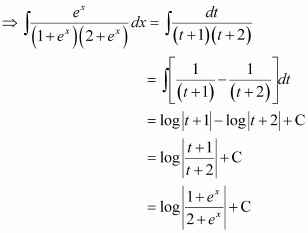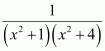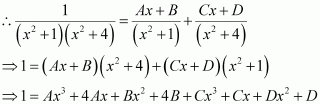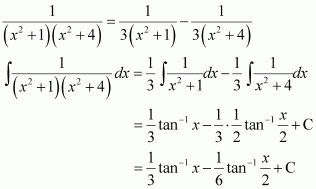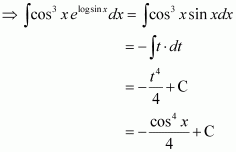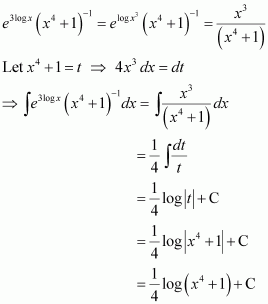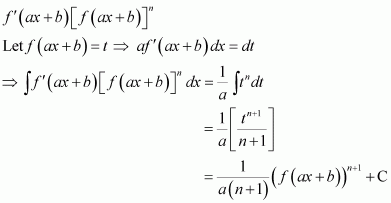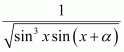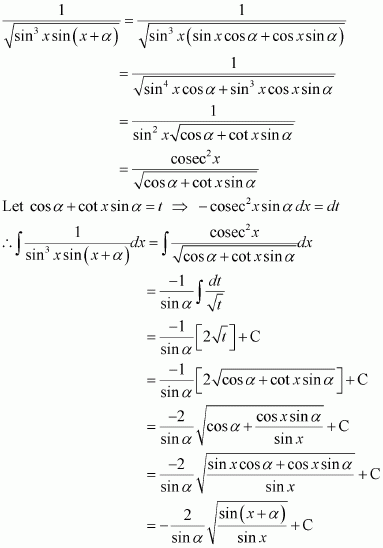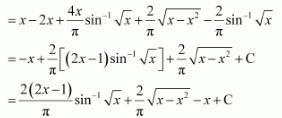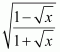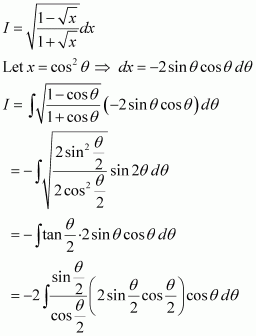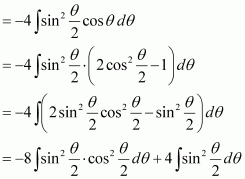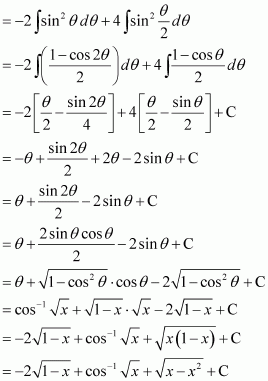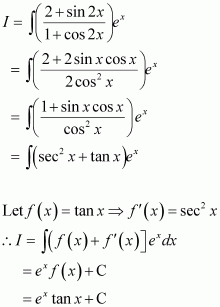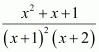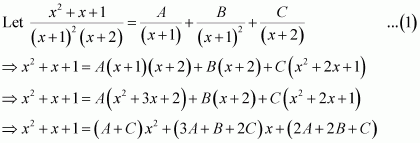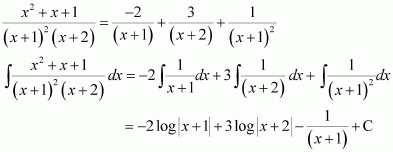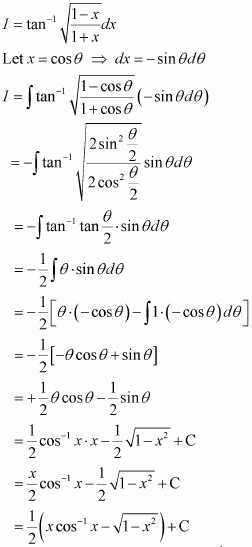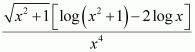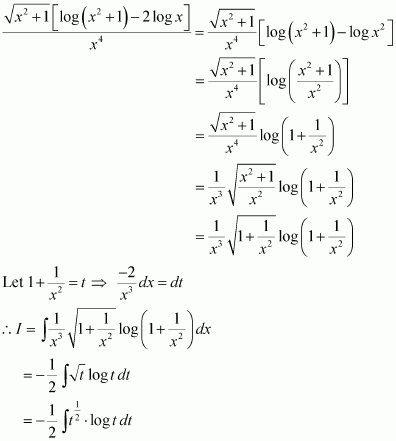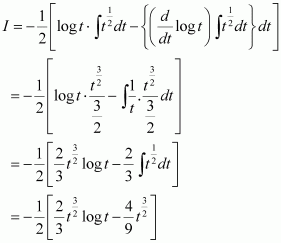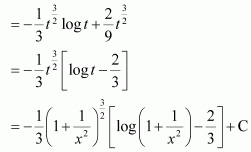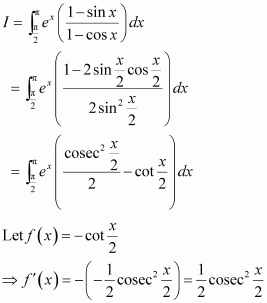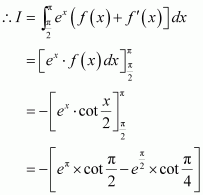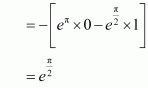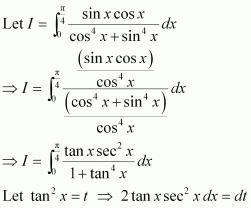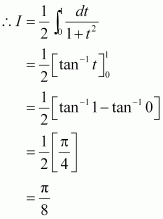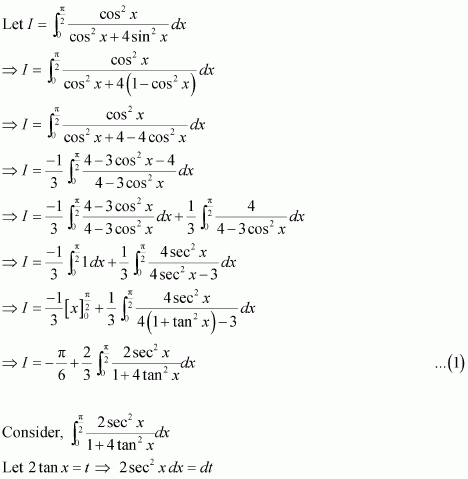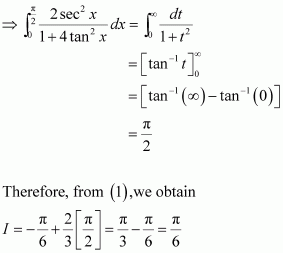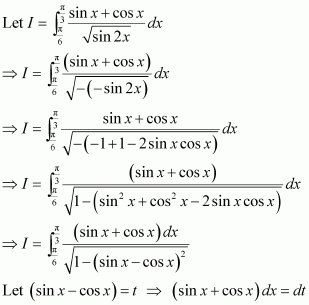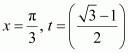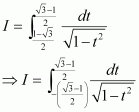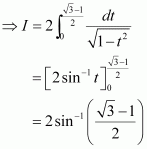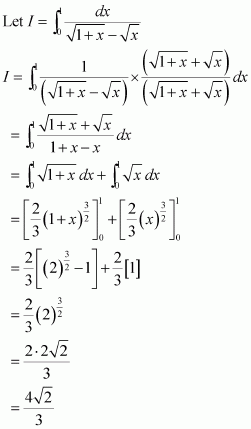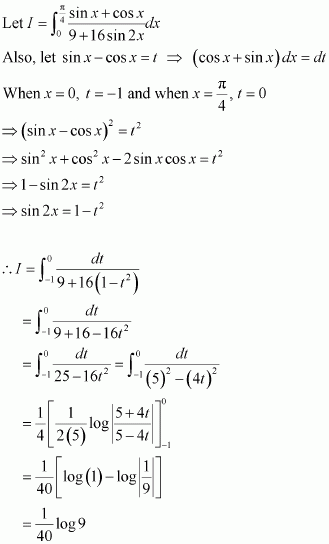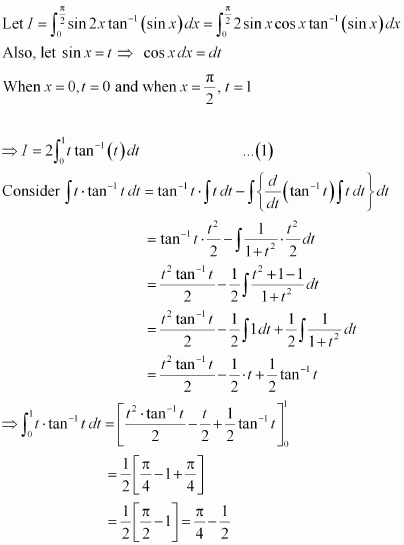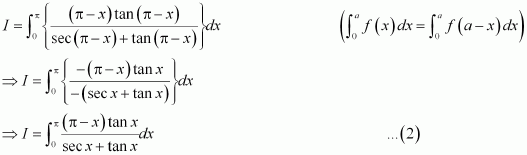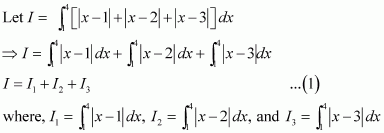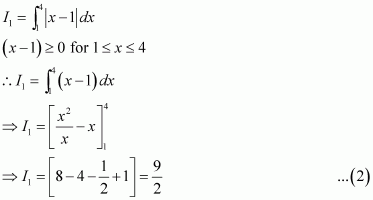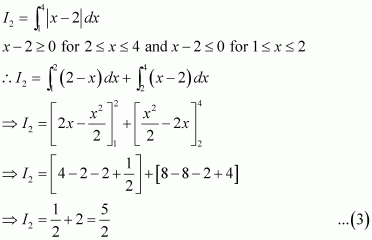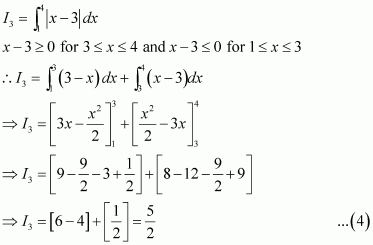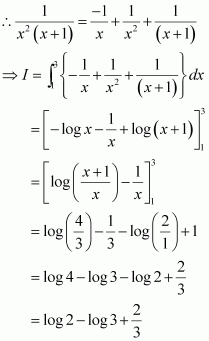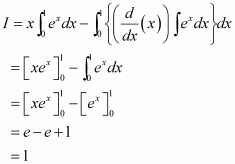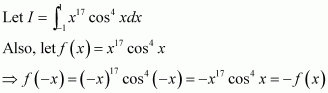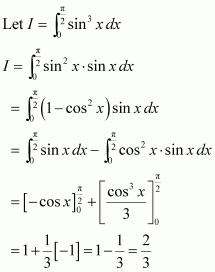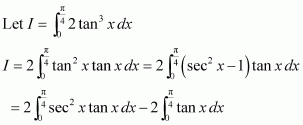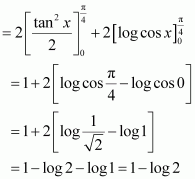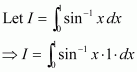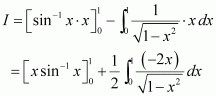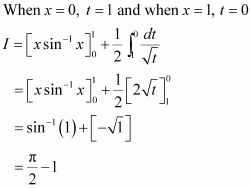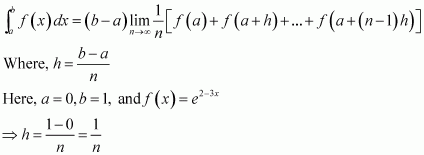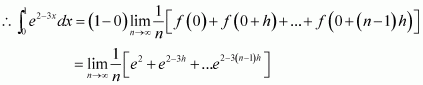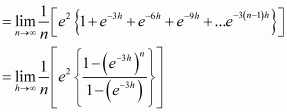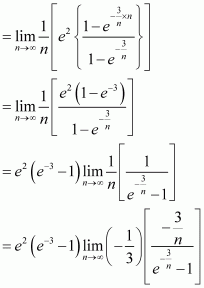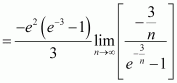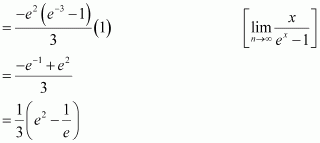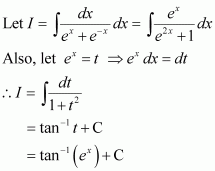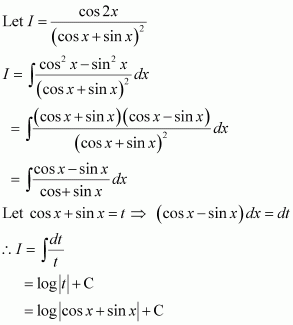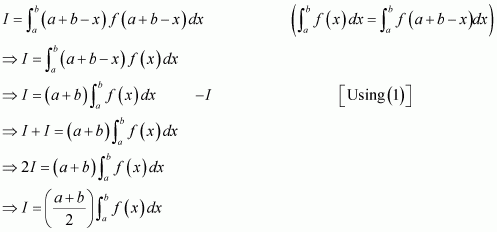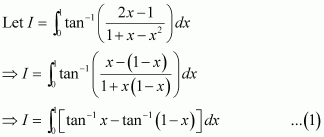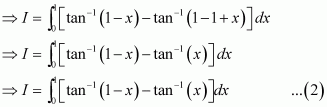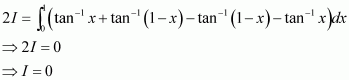NCERT Solutions for Class 12 Maths Chapter 7 – Integrals

Page No 299:

Question 1:

sin 2x

Answer:

The anti derivative of sin 2x is a function of x whose derivative is sin 2x.

It is known that,

Therefore, the anti derivative of

Question 2:

Cos 3x

Answer:

The anti derivative of cos 3x is a function of x whose derivative is cos 3x.

It is known that,

Therefore, the anti derivative of .

Question 3:

e^2x

Answer:

The anti derivative of e^2x is the function of x whose derivative is e^2x.

It is known that,

Therefore, the anti derivative of .

Question 4:

Answer:

The anti derivative of

is the function of x whose derivative is .

It is known that,

Therefore, the anti derivative of .

Question 5:

Answer:

The anti derivative of  is the function of x whose derivative is .

It is known that,

Therefore, the anti derivative of  is .

Question 6:

Answer:

Question 7:

Answer:

Question 8:

Answer:

Question 9:

Answer:

Question 10:

Answer:

Question 11:

Answer:

Question 12:

Answer:

Question 13:

Answer:

On dividing, we obtain

Question 14:

Answer:

Question 15:

Answer:

Question 16:

Answer:

Question 17:

Answer:

Question 18:

Answer:

Question 19:

Answer:

Question 20:

Answer:

Question 21:

The anti derivative of equals

(A)  (B) 

(C)  (D) 

Answer:

Hence, the correct answer is C.

Question 22:

If such that f(2) = 0, then f(x) is

(A)  (B) 

(C)  (D) 

Answer:

It is given that,

∴Anti derivative of 

∴

Also,

Hence, the correct answer is A.

Page No 304:

Question 1:

Answer:

Let = t

∴2x dx = dt

Question 2:

Answer:

Let log |x| = t

∴ 

Question 3:

Answer:

Let 1 + log x = t

∴ 

Question 4:

sin x ⋅ sin (cos x)

Answer:

sin x ⋅ sin (cos x)

Let cos x = t

∴ −sin x dx = dt

Question 5:

Answer:

Let 

∴ 2adx = dt

Question 6:

Answer:

Let ax + b = t

⇒ adx = dt

Question 7:

Answer:

Let 

∴ dx = dt

Question 8:

Answer:

Let 1 + 2x² = t

∴ 4xdx = dt

Question 9:

Answer:

Let 

∴ (2x + 1)dx = dt

Question 10:

Answer:

Let 

∴

Question 11:

Answer:

Let I=∫xx+4 dxput x+4=t⇒dx=dtNow, I=∫t-4tdt=∫t-4t-1/2dt=23t3/2-42t1/2+C=23.t.t1/2-8t1/2+C=23x+4x+4-8x+4+C=23xx+4+83x+4-8x+4+C=23xx+4-163x+4+C=23x+4x-8+C

 

Question 12:

Answer:

Let 

∴ 

Question 13:

Answer:

Let 

∴ 9x² dx = dt

Question 14:

Answer:

Let log x = t

∴ 

Question 15:

Answer:

Let 

∴ −8x dx = dt

Question 16:

Answer:

Let 

∴ 2dx = dt

Question 17:

Answer:

Let 

∴ 2xdx = dt

Page No 305:

Question 18:

Answer:

Let 

∴ 

Question 19:

Answer:

Dividing numerator and denominator by e^x, we obtain

Let 

∴ 

Question 20:

Answer:

Let 

∴ 

Question 21:

Answer:

Let 2x − 3 = t

∴ 2dx = dt

⇒∫tan22x-3dx = ∫sec22x-3 – 1dx=∫sec2t- 1dt2= 12∫sec2t dt – ∫1dt= 12tant – t + C= 12tan2x-3 – 2x-3 + C

Question 22:

Answer:

Let 7 − 4x = t

∴ −4dx = dt

Question 23:

Answer:

Let 

∴ 

Question 24:

Answer:

Let 

∴ 

Question 25:

Answer:

Let 

∴ 

Question 26:

Answer:

Let 

∴ 

Question 27:

Answer:

Let sin 2x = t

∴ 

Question 28:

Answer:

Let 

∴ cos x dx = dt

Question 29:

cot x log sin x

Answer:

Let log sin x = t

Question 30:

Answer:

Let 1 + cos x = t

∴ −sin x dx = dt

Question 31:

Answer:

Let 1 + cos x = t

∴ −sin x dx = dt

Question 32:

Answer:

Let sin x + cos x = t ⇒ (cos x − sin x) dx = dt

Question 33:

Answer:

Put cos x − sin x = t ⇒ (−sin x − cos x) dx = dt

Question 34:

Answer:

Question 35:

Answer:

Let 1 + log x = t

∴ 

Question 36:

Answer:

Let 

∴ 

Question 37:

Answer:

Let x⁴ = t

∴ 4x³ dx = dt

Let 

∴

From (1), we obtain

Question 38:

equals

Answer:

Let 

∴ 

Hence, the correct answer is D.

Question 39:

equals

A. 

B. 

C. 

D. 

Answer:

Hence, the correct answer is B.

Page No 307:

Question 1:

Answer:

Question 2:

Answer:

It is known that, 

Question 3:

cos 2x cos 4x cos 6x

Answer:

It is known that,

Question 4:

sin³ (2x + 1)

Answer:

Let 

Question 5:

sin³ x cos³ x

Answer:

Question 6:

sin x sin 2x sin 3x

Answer:

It is known that, 

Question 7:

sin 4x sin 8x

Answer:

It is known that,

sin A . sin B = 12cosA-B-cosA+B∴∫sin4x sin8x dx=∫12cos4x-8x-cos4x+8xdx=12∫cos-4x-cos12xdx=12∫cos4x-cos12xdx=12sin4x4-sin12x12+C

Question 8:

Answer:

Question 9:

Answer:

Question 10:

sin⁴ x

Answer:

Question 11:

cos⁴ 2x

Answer:

Question 12:

Answer:

Question 13:

Answer:

Question 14:

Answer:

Question 15:

Answer:

Question 16:

tan⁴x

Answer:

From equation (1), we obtain

Question 17:

Answer:

Question 18:

Answer:

Question 19:

Answer:

1sinxcos3x=sin2x+cos2xsinxcos3x=sinxcos3x+1sinxcosx

 

⇒1sinxcos3x=tanxsec2x+1cos2xsinxcosxcos2x=tanxsec2x+sec2xtanx

Question 20:

Answer:

Question 21:

sin⁻¹ (cos x)

Answer:

It is known that,

Substituting in equation (1), we obtain

Question 22:

Answer:

Question 23:

 is equal to

A. tan x + cot x + C

B. tan x + cosec x + C

C. − tan x + cot x + C

D. tan x + sec x + C

Answer:

Hence, the correct answer is A.

Question 24:

 equals

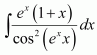
A. âˆ’ cot (e^xx) + C

B. tan (xe^x) + C

C. tan (e^x) + C

D. cot (e^x) + C

Answer:

Let e^xx = t

Hence, the correct answer is B.

Page No 315:

Question 1:

Answer:

Let x³ = t

∴ 3x² dx = dt

Question 2:

Answer:

Let 2x = t

∴ 2dx = dt

Question 3:

Answer:

Let 2 − x = t

⇒ −dx = dt

Question 4:

Answer:

Let 5x = t

∴ 5dx = dt

Question 5:

Answer:

Question 6:

Answer:

Let x³ = t

∴ 3x² dx = dt

Question 7:

Answer:

From (1), we obtain

Question 8:

Answer:

Let x³ = t

⇒ 3x² dx = dt

Question 9:

Answer:

Let tan x = t

∴ sec²x dx = dt

Page No 316:

Question 10:

Answer:

Question 11:

19×2+6x+5

Answer:

∫19×2+6x+5dx=∫13x+12+22dx

 

Let (3x+1)=t

∴

3 dx=dt

 

⇒∫13x+12+22dx=13∫1t2+22dt

 

=13×2tan-1t2+C

 

=16tan-13x+12+C

 

Question 12:

Answer:

Question 13:

Answer:

Question 14:

Answer:

Question 15:

Answer:

Question 16:

Answer:

Equating the coefficients of x and constant term on both sides, we obtain

4A = 4 ⇒ A = 1

A + B = 1 ⇒ B = 0

Let 2x² + x − 3 = t

∴ (4x + 1) dx = dt

Question 17:

Answer:

Equating the coefficients of x and constant term on both sides, we obtain

From (1), we obtain

From equation (2), we obtain

Question 18:

Answer:

Equating the coefficient of x and constant term on both sides, we obtain

Substituting equations (2) and (3) in equation (1), we obtain

Question 19:

Answer:

Equating the coefficients of x and constant term, we obtain

2A = 6 ⇒ A = 3

−9A + B = 7 ⇒ B = 34

∴ 6x + 7 = 3 (2x − 9) + 34

Substituting equations (2) and (3) in (1), we obtain

Question 20:

Answer:

Equating the coefficients of x and constant term on both sides, we obtain

Using equations (2) and (3) in (1), we obtain

Question 21:

Answer:

Let x² + 2x +3 = t

⇒ (2x + 2) dx =dt

Using equations (2) and (3) in (1), we obtain

Question 22:

Answer:

Equating the coefficients of x and constant term on both sides, we obtain

Substituting (2) and (3) in (1), we obtain

Question 23:

Answer:

Equating the coefficients of x and constant term, we obtain

Using equations (2) and (3) in (1), we obtain

Question 24:

equals

A. x tan⁻¹ (x + 1) + C

B. tan^{− 1} (x + 1) + C

C. (x + 1) tan⁻¹ x + C

D. tan⁻¹ x + C

Answer:

Hence, the correct answer is B.

Question 25:

equals

A. 

B. 

C. 

D. 

Answer:

Hence, the correct answer is B.

Page No 322:

Question 1:

Answer:

Let 

Equating the coefficients of x and constant term, we obtain

A + B = 1

2A + B = 0

On solving, we obtain

A = −1 and B = 2

Question 2:

Answer:

Let 

Equating the coefficients of x and constant term, we obtain

A + B = 0

−3A + 3B = 1

On solving, we obtain

Question 3:

Answer:

Let 

Substituting x = 1, 2, and 3 respectively in equation (1), we obtain

A = 1, B = −5, and C = 4

Question 4:

Answer:

Let 

Substituting x = 1, 2, and 3 respectively in equation (1), we obtain 

Question 5:

Answer:

Let 

Substituting x = −1 and −2 in equation (1), we obtain

A = −2 and B = 4

Question 6:

Answer:

It can be seen that the given integrand is not a proper fraction.

Therefore, on dividing (1 − x²) by x(1 − 2x), we obtain

Let 

Substituting x = 0 and  in equation (1), we obtain

A = 2 and B = 3

Substituting in equation (1), we obtain

Question 7:

Answer:

Let 

Equating the coefficients of x², x, and constant term, we obtain

A + C = 0

−A + B = 1

−B + C = 0

On solving these equations, we obtain

From equation (1), we obtain

Question 8:

Answer:

Let 

Substituting x = 1, we obtain

Equating the coefficients of x² and constant term, we obtain

A + C = 0

−2A + 2B + C = 0

On solving, we obtain

Question 9:

Answer:

Let 

Substituting x = 1 in equation (1), we obtain

B = 4

Equating the coefficients of x² and x, we obtain

A + C = 0

B − 2C = 3

On solving, we obtain

Question 10:

Answer:

Let 

Equating the coefficients of x² and x, we obtain

Question 11:

Answer:

Let 

Substituting x = −1, −2, and 2 respectively in equation (1), we obtain

Question 12:

Answer:

It can be seen that the given integrand is not a proper fraction.

Therefore, on dividing (x³ + x + 1) by x² − 1, we obtain

Let 

Substituting x = 1 and −1 in equation (1), we obtain

Question 13:

Answer:

Equating the coefficient of x², x, and constant term, we obtain

A − B = 0

B − C = 0

A + C = 2

On solving these equations, we obtain

A = 1, B = 1, and C = 1

Question 14:

Answer:

Equating the coefficient of x and constant term, we obtain

A = 3

2A + B = −1 ⇒ B = −7

Question 15:

Answer:

Equating the coefficient of x³, x², x, and constant term, we obtain

On solving these equations, we obtain

Question 16:

 [Hint: multiply numerator and denominator by x^{n − 1} and put xⁿ = t]

Answer:

Multiplying numerator and denominator by x^{n − 1}, we obtain

Substituting t = 0, −1 in equation (1), we obtain

A = 1 and B = −1

Question 17:

 [Hint: Put sin x = t]

Answer:

Substituting t = 2 and then t = 1 in equation (1), we obtain

A = 1 and B = −1

Page No 323:

Question 18:

Answer:

Equating the coefficients of x³, x², x, and constant term, we obtain

A + C = 0

B + D = 4

4A + 3C = 0

4B + 3D = 10

On solving these equations, we obtain

A = 0, B = −2, C = 0, and D = 6

Question 19:

Answer:

Let x² = t ⇒ 2x dx = dt

Substituting t = −3 and t = −1 in equation (1), we obtain

Question 20:

Answer:

Multiplying numerator and denominator by x³, we obtain

Let x⁴ = t ⇒ 4x³dx = dt

Substituting t = 0 and 1 in (1), we obtain

A = −1 and B = 1

Question 21:

 [Hint: Put e^x = t]

Answer:

Let e^x = t ⇒ e^x dx = dt

Substituting t = 1 and t = 0 in equation (1), we obtain

A = −1 and B = 1

Question 22:

A. 

B. 

C. 

D. 

Answer:

Substituting x = 1 and 2 in (1), we obtain

A = −1 and B = 2

Hence, the correct answer is B.

Question 23:

A. 

B. 

C. 

D. 

Answer:

Equating the coefficients of x², x, and constant term, we obtain

A + B = 0

C = 0

A = 1

On solving these equations, we obtain

A = 1, B = −1, and C = 0

Hence, the correct answer is A.

Page No 327:

Question 1:

x sin x

Answer:

Let I = 

Taking x as first function and sin x as second function and integrating by parts, we obtain

Question 2:

Answer:

Let I = 

Taking x as first function and sin 3x as second function and integrating by parts, we obtain

Question 3:

Answer:

Let 

Taking x² as first function and e^x as second function and integrating by parts, we obtain

Again integrating by parts, we obtain

Question 4:

x logx

Answer:

Let 

Taking log x as first function and x as second function and integrating by parts, we obtain

Question 5:

x log 2x

Answer:

Let 

Taking log 2x as first function and x as second function and integrating by parts, we obtain

Question 6:

x² log x

Answer:

Let 

Taking log x as first function and x² as second function and integrating by parts, we obtain

Question 7:

Answer:

Let 

Taking as first function and x as second function and integrating by parts, we obtain

Question 8:

Answer:

Let 

Taking  as first function and x as second function and integrating by parts, we obtain

Question 9:

Answer:

Let 

Taking cos⁻¹ x as first function and x as second function and integrating by parts, we obtain

Question 10:

Answer:

Let 

Taking  as first function and 1 as second function and integrating by parts, we obtain

Question 11:

Answer:

Let 

Taking  as first function and  as second function and integrating by parts, we obtain

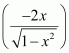
Question 12:

Answer:

Let 

Taking x as first function and sec²x as second function and integrating by parts, we obtain

Question 13:

Answer:

Let 

Taking  as first function and 1 as second function and integrating by parts, we obtain

Question 14:

Answer:

Taking  as first function and x as second function and integrating by parts, we obtain

I=log x 2∫xdx-∫ddxlog x 2∫xdxdx=x22log x 2-∫2log x .1x.x22dx=x22log x 2-∫xlog x dx

Again integrating by parts, we obtain

I = x22logx 2-log x ∫x dx-∫ddxlog x ∫x dxdx=x22logx 2-x22log x -∫1x.x22dx=x22logx 2-x22log x +12∫x dx=x22logx 2-x22log x +x24+C

Question 15:

Answer:

Let 

Let I = I₁ + I₂ … (1)

Where, and 

Taking log x as first function and x² as second function and integrating by parts, we obtain

Taking log x as first function and 1 as second function and integrating by parts, we obtain

Using equations (2) and (3) in (1), we obtain

Page No 328:

Question 16:

Answer:

Let 

Let

⇒ 

∴ 

It is known that, 

Question 17:

Answer:

Let 

Let  ⇒ 

It is known that, 

Question 18:

Answer:

Let  ⇒ 

It is known that, 

From equation (1), we obtain

Question 19:

Answer:

Also, let  ⇒ 

It is known that, 

Question 20:

Answer:

Let  ⇒ 

It is known that, 

Question 21:

Answer:

Let

Integrating by parts, we obtain

Again integrating by parts, we obtain

Question 22:

Answer:

Let ⇒ 

 = 2θ

⇒ 

Integrating by parts, we obtain

Question 23:

 equals

Answer:

Let 

Also, let  ⇒ 

Hence, the correct answer is A.

Question 24:

 equals

Answer:

Let 

Also, let  ⇒ 

It is known that, 

Hence, the correct answer is B.

Page No 330:

Question 1:

Answer:

 

 

Question 2:

Answer:

Question 3:

Answer:

Question 4:

Answer:

Question 5:

Answer:

Question 6:

Answer:

Question 7:

Answer:

Question 8:

Answer:

Question 9:

Answer:

Question 10:

is equal to

A. 

B. 

C. 

D. 

Answer:

Hence, the correct answer is A.

Question 11:

is equal to

A. 

B. 

C. 

D. 

Answer:

Hence, the correct answer is D.

Page No 334:

Question 1:

Answer:

It is known that,

Question 2:

Answer:

It is known that,

Question 3:

Answer:

It is known that,

Question 4:

Answer:

It is known that,

From equations (2) and (3), we obtain

Question 5:

Answer:

It is known that,

Question 6:

Answer:

It is known that,

Page No 338:

Question 1:

Answer:

By second fundamental theorem of calculus, we obtain

Question 2:

Answer:

By second fundamental theorem of calculus, we obtain

Question 3:

Answer:

By second fundamental theorem of calculus, we obtain

Question 4:

Answer:

By second fundamental theorem of calculus, we obtain

Question 5:

Answer:

By second fundamental theorem of calculus, we obtain

Question 6:

Answer:

By second fundamental theorem of calculus, we obtain

Question 7:

Answer:

By second fundamental theorem of calculus, we obtain

Question 8:

Answer:

By second fundamental theorem of calculus, we obtain

Question 9:

Answer:

By second fundamental theorem of calculus, we obtain

Question 10:

Answer:

By second fundamental theorem of calculus, we obtain

Question 11:

Answer:

By second fundamental theorem of calculus, we obtain

Question 12:

Answer:

By second fundamental theorem of calculus, we obtain

Question 13:

Answer:

By second fundamental theorem of calculus, we obtain

Question 14:

Answer:

By second fundamental theorem of calculus, we obtain

Question 15:

Answer:

By second fundamental theorem of calculus, we obtain

Question 16:

Answer:

Let 

Equating the coefficients of x and constant term, we obtain

A = 10 and B = −25

Substituting the value of I₁ in (1), we obtain

Question 17:

Answer:

By second fundamental theorem of calculus, we obtain

Question 18:

Answer:

By second fundamental theorem of calculus, we obtain

Question 19:

Answer:

By second fundamental theorem of calculus, we obtain

Question 20:

Answer:

By second fundamental theorem of calculus, we obtain

Question 21:

equals

A. 

B. 

C. 

D. 

Answer:

By second fundamental theorem of calculus, we obtain

Hence, the correct answer is D.

Question 22:

equals

A. 

B. 

C. 

D. 

Answer:

By second fundamental theorem of calculus, we obtain

Hence, the correct answer is C.

Page No 340:

Question 1:

Answer:

When x = 0, t = 1 and when x = 1, t = 2

Question 2:

Answer:

Also, let 

Question 3:

Answer:

Also, let x = tanθ ⇒ dx = sec²θ dθ

When x = 0, θ = 0 and when x = 1, 

Takingθas first function and sec²θ as second function and integrating by parts, we obtain

Question 4:

Answer:

Let x + 2 = t² ⇒ dx = 2tdt

When x = 0,  and when x = 2, t = 2

Question 5:

Answer:

Let cos x = t ⇒ −sinx dx = dt

When x = 0, t = 1 and when

Question 6:

Answer:

Let ⇒ dx = dt

Question 7:

Answer:

Let x + 1 = t ⇒ dx = dt

When x = −1, t = 0 and when x = 1, t = 2

Question 8:

Answer:

Let 2x = t ⇒ 2dx = dt

When x = 1, t = 2 and when x = 2, t = 4

Question 9:

The value of the integral 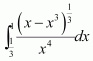 is

A. 6

B. 

C. 3

D. 4

Answer:

Let cotθ = t ⇒ −cosec2θ dθ= dt

Hence, the correct answer is A.

Question 10:

If 

A. cos x + x sin x

B. x sin x

C. x cos x

D. sin x + x cos x

Answer:

Integrating by parts, we obtain

Hence, the correct answer is B.

Page No 347:

Question 1:

Answer:

Adding (1) and (2), we obtain

Question 2:

Answer:

Adding (1) and (2), we obtain

Question 3:

Answer:

Adding (1) and (2), we obtain

Question 4:

Answer:

Adding (1) and (2), we obtain

Question 5:

Answer:

It can be seen that (x + 2) ≤ 0 on [−5, −2] and (x + 2) ≥ 0 on [−2, 5].

Question 6:

Answer:

It can be seen that (x − 5) ≤ 0 on [2, 5] and (x − 5) ≥ 0 on [5, 8].

Question 7:

Answer:

Question 8:

Answer:

Question 9:

Answer:

Question 10:

Answer:

Adding (1) and (2), we obtain

Question 11:

Answer:

As sin² (−x) = (sin (−x))² = (−sin x)² = sin²x, therefore, sin²x is an even function.

It is known that if f(x) is an even function, then 

Question 12:

Answer:

Adding (1) and (2), we obtain

Question 13:

Answer:

As sin⁷ (−x) = (sin (−x))⁷ = (−sin x)⁷ = −sin⁷x, therefore, sin²x is an odd function.

It is known that, if f(x) is an odd function, then 

Question 14:

Answer:

It is known that,

Question 15:

Answer:

Adding (1) and (2), we obtain

Question 16:

Answer:

Adding (1) and (2), we obtain

sin (π − x) = sin x

Adding (4) and (5), we obtain

Let 2x = t ⇒ 2dx = dt

When x = 0, t = 0 and when

x=π2, t=π∴

I=12∫0πlog sin tdt-π2log 2

⇒I=I2-π2log 2       [from 3]

⇒I2=-π2log 2

⇒I=-πlog 2

Question 17:

Answer:

It is known that, 

Adding (1) and (2), we obtain

Question 18:

Answer:

It can be seen that, (x − 1) ≤ 0 when 0 ≤ x ≤ 1 and (x − 1) ≥ 0 when 1 ≤ x ≤ 4

Question 19:

Show that if f and g are defined as and 

Answer:

Adding (1) and (2), we obtain

Question 20:

The value of is

A. 

B. 2

C. π

D. 1

Answer:

It is known that if f(x) is an even function, then  and

if f(x) is an odd function, then 

Hence, the correct answer is C.

Question 21:

The value of is

A. 2

B. 

C. 0

D. 

Answer:

Adding (1) and (2), we obtain

Hence, the correct answer is C.

Page No 352:

Question 1:

Answer:

Equating the coefficients of x², x, and constant term, we obtain

−A + B − C = 0

B + C = 0

A = 1

On solving these equations, we obtain

From equation (1), we obtain

Question 2:

Answer:

Question 3:

 [Hint: Put]

Answer:

Question 4:

Answer:

Question 5:

 

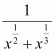
Answer:

On dividing, we obtain

Question 6:

Answer:

Equating the coefficients of x², x, and constant term, we obtain

A + B = 0

B + C = 5

9A + C = 0

On solving these equations, we obtain

From equation (1), we obtain

Question 7:

Answer:

Let x − a = t ⇒ dx = dt

Question 8:

Answer:

Question 9:

Answer:

Let sin x = t ⇒ cos x dx = dt

Question 10:

Answer:

Question 11:

Answer:

Question 12:

Answer:

Let x⁴ = t ⇒ 4x³ dx = dt

Question 13:

Answer:

Let e^x = t ⇒ e^x dx = dt

Question 14:

Answer:

Equating the coefficients of x³, x², x, and constant term, we obtain

A + C = 0

B + D = 0

4A + C = 0

4B + D = 1

On solving these equations, we obtain

From equation (1), we obtain

Question 15:

Answer:

= cos³ x × sin x

Let cos x = t ⇒ −sin x dx = dt

Question 16:

Answer:

Question 17:

Answer:

Question 18:

Answer:

Question 19:

Answer:

Let I=∫sin-1x-cos-1xsin-1x+cos-1xdx

 

It is known that, sin-1x+cos-1x=π2

 

⇒I=∫π2-cos-1x-cos-1xπ2dx

 

=2π∫π2-2cos-1xdx

 

=2π.π2∫1.dx-4π∫cos-1xdx

 

=x-4π∫cos-1xdx           …(1)

 

Let I1=∫cos-1x dx

 

Also, let x=t⇒dx=2 t dt

 

⇒I1=2∫cos-1t.t dt

 

=2cos-1t.t22-∫-11-t2.t22dt

 

=t2cos-1t+∫t21-t2dt

 

=t2cos-1t-∫1-t2-11-t2dt

 

=t2cos-1t-∫1-t2dt+∫11-t2dt

 

=t2cos-1t-t21-t2-12sin-1t+sin-1t

 

=t2cos-1t-t21-t2+12sin-1t

From equation (1), we obtain

I=x-4πt2cos-1t-t21-t2+12sin-1t  =x-4πxcos-1x-x21-x+12sin-1x

=x-4πxπ2-sin-1x-x-x22+12sin-1x 

Question 20:

Answer:

Question 21:

Answer:

Question 22:

Answer:

Equating the coefficients of x², x,and constant term, we obtain

A + C = 1

3A + B + 2C = 1

2A + 2B + C = 1

On solving these equations, we obtain

A = −2, B = 1, and C = 3

From equation (1), we obtain

Page No 353:

Question 23:

Answer:

Question 24:

Answer:

Integrating by parts, we obtain

Question 25:

Answer:

Question 26:

Answer:

When x = 0, t = 0 and 

Question 27:

Answer:

When and when

Question 28:

Answer:

When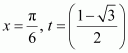 and when 

As 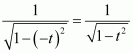, therefore, is an even function.

It is known that if f(x) is an even function, then 

Question 29:

Answer:

Question 30:

Answer:

Question 31:

Answer:

From equation (1), we obtain

Question 32:

Answer:

Adding (1) and (2), we obtain

Question 33:

Answer:

From equations (1), (2), (3), and (4), we obtain

Question 34:

Answer:

Equating the coefficients of x², x, and constant term, we obtain

A + C = 0

A + B = 0

B = 1

On solving these equations, we obtain

A = −1, C = 1, and B = 1

Hence, the given result is proved.

Question 35:

Answer:

Integrating by parts, we obtain

Hence, the given result is proved.

Question 36:

Answer:

Therefore, f (x) is an odd function.

It is known that if f(x) is an odd function, then 

Hence, the given result is proved.

Question 37:

Answer:

Hence, the given result is proved.

Question 38:

Answer:

Hence, the given result is proved.

Question 39:

Answer:

Integrating by parts, we obtain

Let 1 − x² = t ⇒ −2x dx = dt

Hence, the given result is proved.

Question 40:

Evaluate as a limit of a sum.

Answer:

It is known that,

Question 41:

is equal to

A. 

B. 

C. 

D. 

Answer:

Hence, the correct answer is A.

Question 42:

is equal to

A. 

B. 

C. 

D. 

Answer:

Hence, the correct answer is B.

Page No 354:

Question 43:

If then is equal to

A. 

B. 

C. 

D. 

Answer:

Hence, the correct answer is D.

Question 44:

The value of is

A. 1

B. 0

C. − 1

D. 

Answer:

Adding (1) and (2), we obtain

Hence, the correct answer is B.