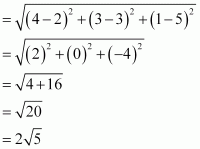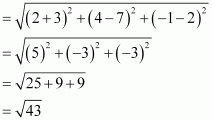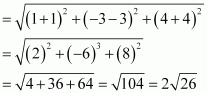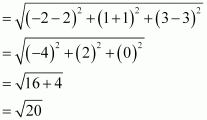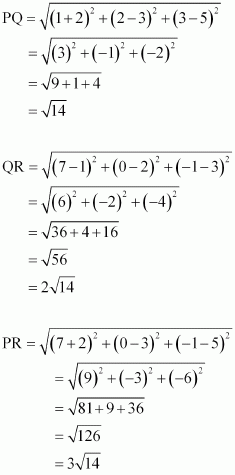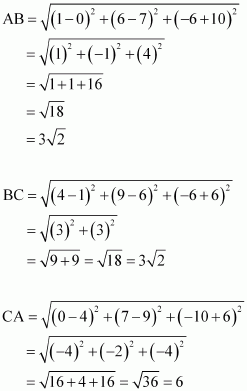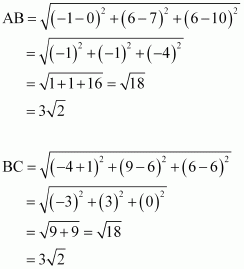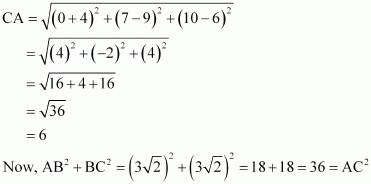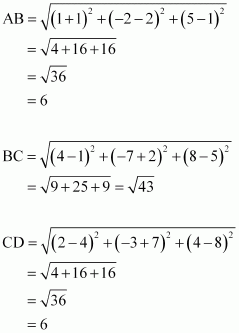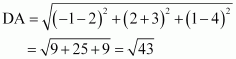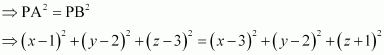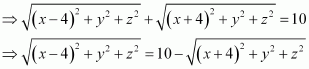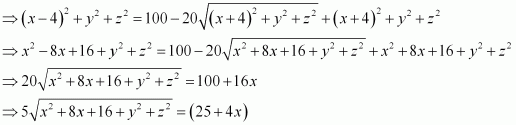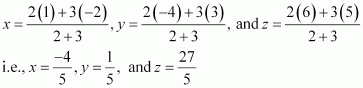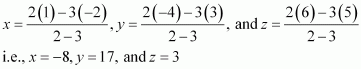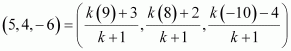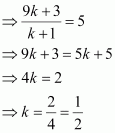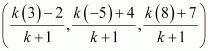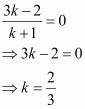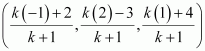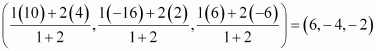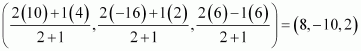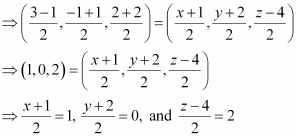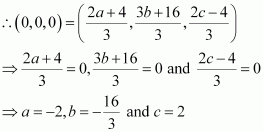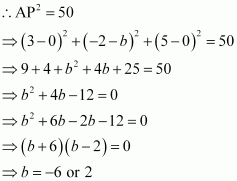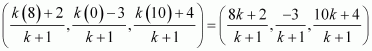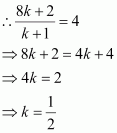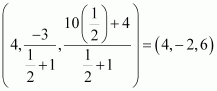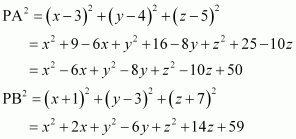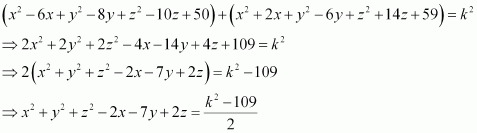NCERT Solutions for Class 11 Maths Chapter 12 – Introduction To Three Dimensional Geometry
Page No 271:
Question 1:
A point is on the x-axis. What are its y-coordinates and z-coordinates?
ANSWER:
If a point is on the x-axis, then its y-coordinates and z-coordinates are zero.
Page No 271:
Question 2:
A point is in the XZ-plane. What can you say about its y-coordinate?
ANSWER:
If a point is in the XZ plane, then its y-coordinate is zero.
Page No 271:
Question 3:
Name the octants in which the following points lie:
(1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (–4, 2, –5), (–4, 2, 5),
(–3, –1, 6), (2, –4, –7)
ANSWER:
The x-coordinate, y-coordinate, and z-coordinate of point (1, 2, 3) are all positive. Therefore, this point lies in octant I.
The x-coordinate, y-coordinate, and z-coordinate of point (4, –2, 3) are positive, negative, and positive respectively. Therefore, this point lies in octant IV.
The x-coordinate, y-coordinate, and z-coordinate of point (4, –2, –5) are positive, negative, and negative respectively. Therefore, this point lies in octant VIII.
The x-coordinate, y-coordinate, and z-coordinate of point (4, 2, –5) are positive, positive, and negative respectively. Therefore, this point lies in octant V.
The x-coordinate, y-coordinate, and z-coordinate of point (–4, 2, –5) are negative, positive, and negative respectively. Therefore, this point lies in octant VI.
The x-coordinate, y-coordinate, and z-coordinate of point (–4, 2, 5) are negative, positive, and positive respectively. Therefore, this point lies in octant II.
The x-coordinate, y-coordinate, and z-coordinate of point (–3, –1, 6) are negative, negative, and positive respectively. Therefore, this point lies in octant III.
The x-coordinate, y-coordinate, and z-coordinate of point (2, –4, –7) are positive, negative, and negative respectively. Therefore, this point lies in octant VIII.
Page No 271:
Question 4:
Fill in the blanks:
(i) The x-axis and y-axis taken together determine a plane known as ___________.
(ii) The coordinates of points in the XY-plane are of the form _______.
(iii) Coordinate planes divide the space into _________ octants.
ANSWER:
(i) The x-axis and y-axis taken together determine a plane known as .
(ii) The coordinates of points in the XY-plane are of the form.
(iii) Coordinate planes divide the space into octants.
Page No 273:
Question 1:
Find the distance between the following pairs of points:
(i) (2, 3, 5) and (4, 3, 1) (ii) (–3, 7, 2) and (2, 4, –1)
(iii) (–1, 3, –4) and (1, –3, 4) (iv) (2, –1, 3) and (–2, 1, 3)
ANSWER:
The distance between points P(x1, y1, z1) and P(x2, y2, z2) is given by
(i) Distance between points (2, 3, 5) and (4, 3, 1)
(ii) Distance between points (–3, 7, 2) and (2, 4, –1)
(iii) Distance between points (–1, 3, –4) and (1, –3, 4)
(iv) Distance between points (2, –1, 3) and (–2, 1, 3)
Page No 273:
Question 2:
Show that the points (–2, 3, 5), (1, 2, 3) and (7, 0, –1) are collinear.
ANSWER:
Let points (–2, 3, 5), (1, 2, 3), and (7, 0, –1) be denoted by P, Q, and R respectively.
Points P, Q, and R are collinear if they lie on a line.
Here, PQ + QR = PR
Hence, points P(–2, 3, 5), Q(1, 2, 3), and R(7, 0, –1) are collinear.
Page No 273:
Question 3:
Verify the following:
(i) (0, 7, –10), (1, 6, –6) and (4, 9, –6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (–1, 6, 6) and (–4, 9, 6) are the vertices of a right angled triangle.
(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are the vertices of a parallelogram.
ANSWER:
(i) Let points (0, 7, –10), (1, 6, –6), and (4, 9, –6) be denoted by A, B, and C respectively.
Here, AB = BC ≠ CA
Thus, the given points are the vertices of an isosceles triangle.
(ii) Let (0, 7, 10), (–1, 6, 6), and (–4, 9, 6) be denoted by A, B, and C respectively.
Therefore, by Pythagoras theorem, ABC is a right triangle.
Hence, the given points are the vertices of a right-angled triangle.
(iii) Let (–1, 2, 1), (1, –2, 5), (4, –7, 8), and (2, –3, 4) be denoted by A, B, C, and D respectively.
Here, AB = CD = 6, BC = AD =
Hence, the opposite sides of quadrilateral ABCD, whose vertices are taken in order, are equal.
Therefore, ABCD is a parallelogram.
Hence, the given points are the vertices of a parallelogram.
Page No 273:
Question 4:
Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, –1).
ANSWER:
Let P (x, y, z) be the point that is equidistant from points A(1, 2, 3) and B(3, 2, –1).
Accordingly, PA = PB
⇒ x2 – 2x + 1 + y2 – 4y + 4 + z2 – 6z + 9 = x2 – 6x + 9 + y2 – 4y + 4 + z2 + 2z + 1
⇒ –2x –4y – 6z + 14 = –6x – 4y + 2z + 14
⇒ – 2x – 6z + 6x – 2z = 0
⇒ 4x – 8z = 0
⇒ x – 2z = 0
Thus, the required equation is x – 2z = 0.
Page No 273:
Question 5:
Find the equation of the set of points P, the sum of whose distances from A (4, 0, 0) and B (–4, 0, 0) is equal to 10.
ANSWER:
Let the coordinates of P be (x, y, z).
The coordinates of points A and B are (4, 0, 0) and (–4, 0, 0) respectively.
It is given that PA + PB = 10.
On squaring both sides, we obtain
On squaring both sides again, we obtain
25 (x2 + 8x + 16 + y2 + z2) = 625 + 16x2 + 200x
⇒ 25x2 + 200x + 400 + 25y2 + 25z2 = 625 + 16x2 + 200x
⇒ 9x2 + 25y2 + 25z2 – 225 = 0
Thus, the required equation is 9x2 + 25y2 + 25z2 – 225 = 0.
Page No 277:
Question 1:
Find the coordinates of the point which divides the line segment joining the points (–2, 3, 5) and (1, –4, 6) in the ratio (i) 2:3 internally, (ii) 2:3 externally.
ANSWER:
(i) The coordinates of point R that divides the line segment joining points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m: n are
.
Let R (x, y, z) be the point that divides the line segment joining points(–2, 3, 5) and (1, –4, 6) internally in the ratio 2:3
Thus, the coordinates of the required point are.
(ii) The coordinates of point R that divides the line segment joining points P (x1, y1, z1) and Q (x2, y2, z2) externally in the ratio m: n are
.
Let R (x, y, z) be the point that divides the line segment joining points(–2, 3, 5) and (1, –4, 6) externally in the ratio 2:3
Thus, the coordinates of the required point are (–8, 17, 3).
Page No 277:
Question 2:
Given that P (3, 2, –4), Q (5, 4, –6) and R (9, 8, –10) are collinear. Find the ratio in which Q divides PR.
ANSWER:
Let point Q (5, 4, –6) divide the line segment joining points P (3, 2, –4) and R (9, 8, –10) in the ratio k:1.
Therefore, by section formula,
Thus, point Q divides PR in the ratio 1:2.
Page No 277:
Question 3:
Find the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8).
ANSWER:
Let the YZ planedivide the line segment joining points (–2, 4, 7) and (3, –5, 8) in the ratio k:1.
Hence, by section formula, the coordinates of point of intersection are given by
On the YZ plane, the x-coordinate of any point is zero.
Thus, the YZ plane divides the line segment formed by joining the given points in the ratio 2:3.
Page No 277:
Question 4:
Using section formula, show that the points A (2, –3, 4), B (–1, 2, 1) and are collinear.
ANSWER:
The given points are A (2, –3, 4), B (–1, 2, 1), and.
Let P be a point that divides AB in the ratio k:1.
Hence, by section formula, the coordinates of P are given by
Now, we find the value of k at which point P coincides with point C.
By taking, we obtain k = 2.
For k = 2, the coordinates of point P are.
i.e., is a point that divides AB externally in the ratio 2:1 and is the same as point P.
Hence, points A, B, and C are collinear.
Page No 277:
Question 5:
Find the coordinates of the points which trisect the line segment joining the points P (4, 2, –6) and Q (10, –16, 6).
ANSWER:
Let A and B be the points that trisect the line segment joining points P (4, 2, –6) and Q (10, –16, 6)
Point A divides PQ in the ratio 1:2. Therefore, by section formula, the coordinates of point A are given by
Point B divides PQ in the ratio 2:1. Therefore, by section formula, the coordinates of point B are given by
Thus, (6, –4, –2) and (8, –10, 2) are the points that trisect the line segment joining points P (4, 2, –6) and Q (10, –16, 6).
Page No 278:
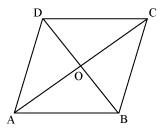
Question 1:
Three vertices of a parallelogram ABCD are A (3, –1, 2), B (1, 2, –4) andC (–1, 1, 2). Find the coordinates of the fourth vertex.
ANSWER:
The three vertices of a parallelogram ABCD are given as A (3, –1, 2), B (1, 2, –4), and C (–1, 1, 2). Let the coordinates of the fourth vertex be D (x, y, z).
We know that the diagonals of a parallelogram bisect each other.
Therefore, in parallelogram ABCD, AC and BD bisect each other.
∴Mid-point of AC = Mid-point of BD
⇒ x = 1, y = –2, and z = 8
Thus, the coordinates of the fourth vertex are (1, –2, 8).
Page No 278:
Question 2:
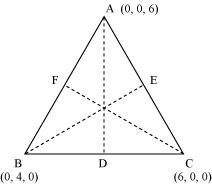
Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0, 4, 0) and (6, 0, 0).
ANSWER:
Let AD, BE, and CF be the medians of the given triangle ABC.
Since AD is the median, D is the mid-point of BC.
∴Coordinates of point D == (3, 2, 0)
Thus, the lengths of the medians of ΔABC are.
Page No 278:
Question 3:
If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (–4, 3b, –10) and R (8, 14, 2c), then find the values of a, b and c.
ANSWER:
It is known that the coordinates of the centroid of the triangle, whose vertices are (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3), are.
Therefore, coordinates of the centroid of ΔPQR
It is given that origin is the centroid of ΔPQR.
Thus, the respective values of a, b, and c are
Page No 279:
Question 4:
Find the coordinates of a point on y-axis which are at a distance offrom the point P (3, –2, 5).
ANSWER:
If a point is on the y-axis, then x-coordinate and the z-coordinate of the point are zero.
Let A (0, b, 0) be the point on the y-axis at a distance of from point P (3, –2, 5). Accordingly,
Thus, the coordinates of the required points are (0, 2, 0) and (0, –6, 0).
Page No 279:
Question 5:
A point R with x-coordinate 4 lies on the line segment joining the pointsP (2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.
[Hint suppose R divides PQ in the ratio k: 1. The coordinates of the point R are given by
ANSWER:
The coordinates of points P and Q are given as P (2, –3, 4) and Q (8, 0, 10).
Let R divide line segment PQ in the ratio k:1.
Hence, by section formula, the coordinates of point R are given by
It is given that the x-coordinate of point R is 4.
Therefore, the coordinates of point R are
Page No 279:
Question 6:
If A and B be the points (3, 4, 5) and (–1, 3, –7), respectively, find the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant.
ANSWER:
The coordinates of points A and B are given as (3, 4, 5) and (–1, 3, –7) respectively.
Let the coordinates of point P be (x, y, z).
On using distance formula, we obtain
Now, if PA2 + PB2 = k2, then
Thus, the required equation is.