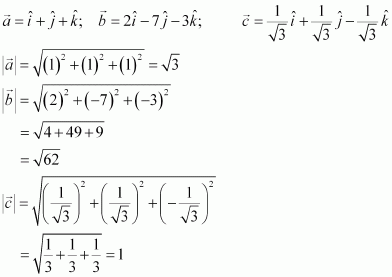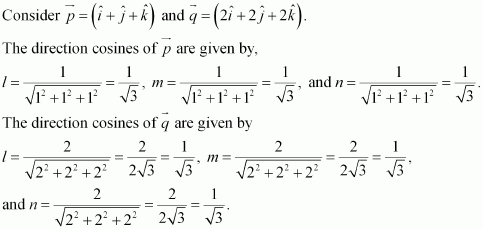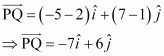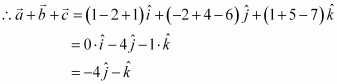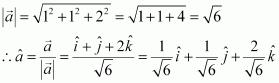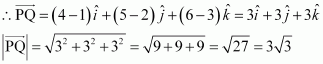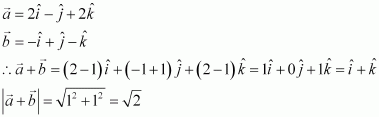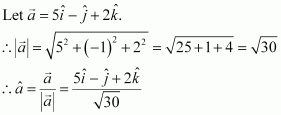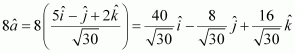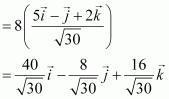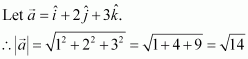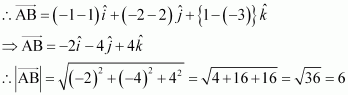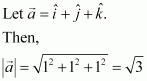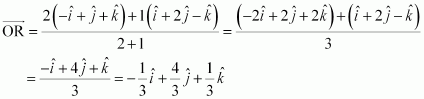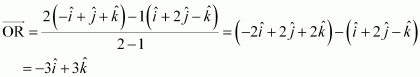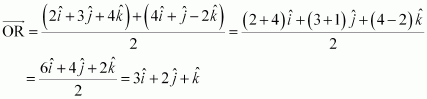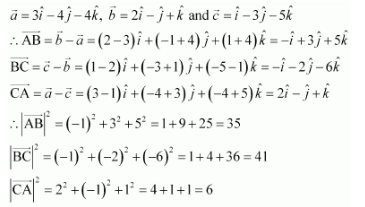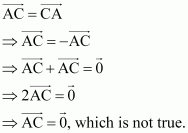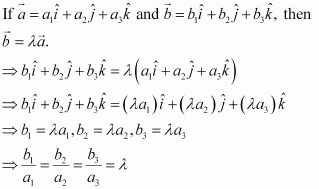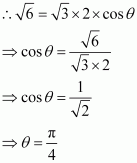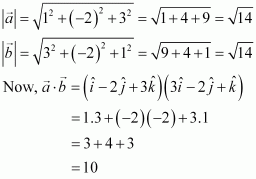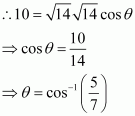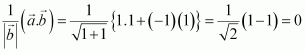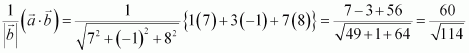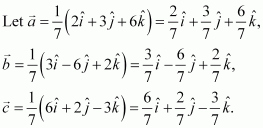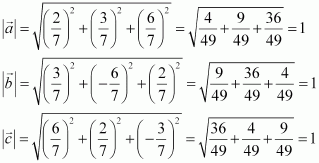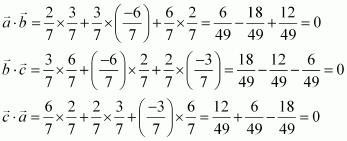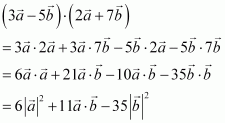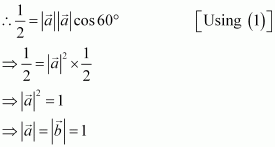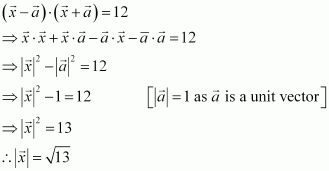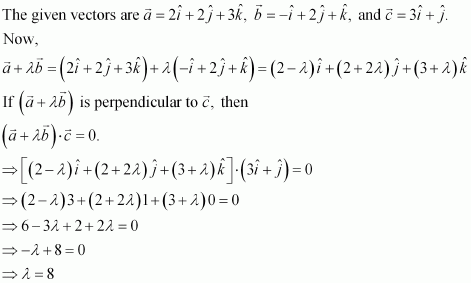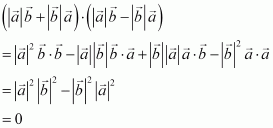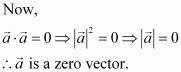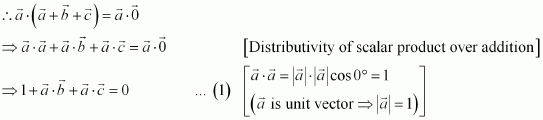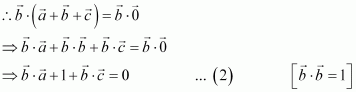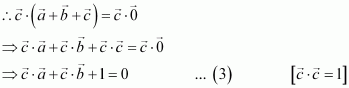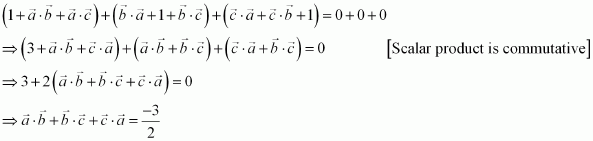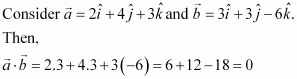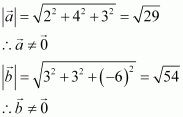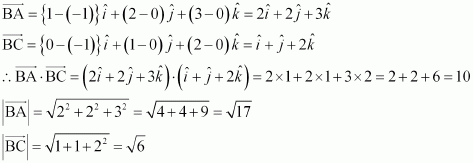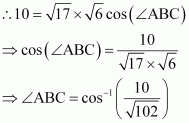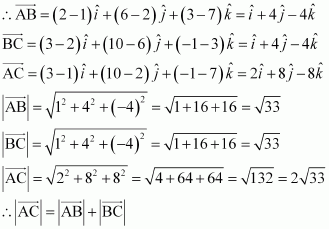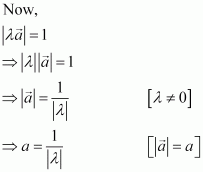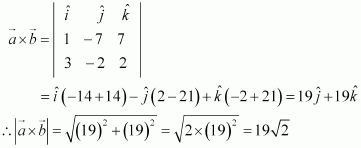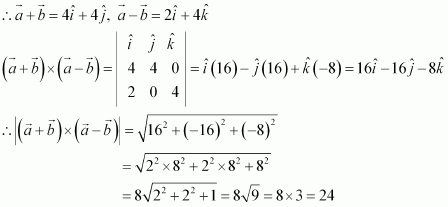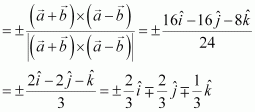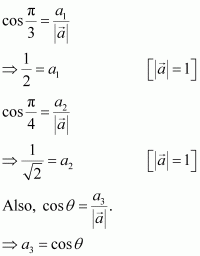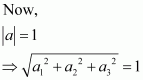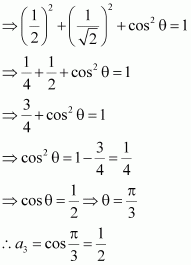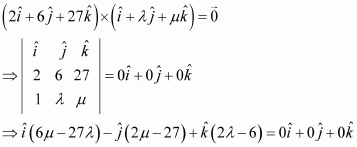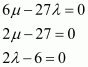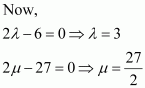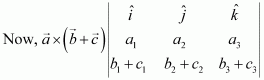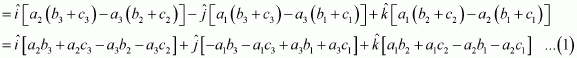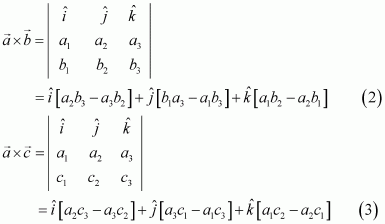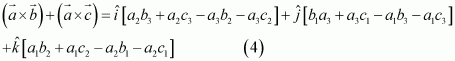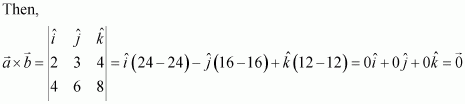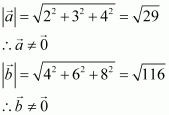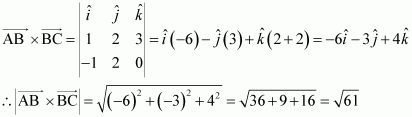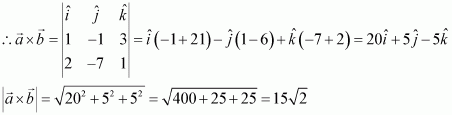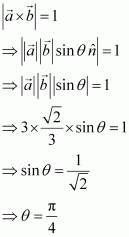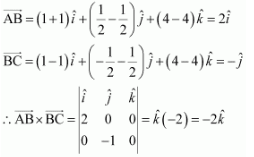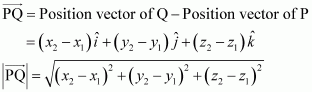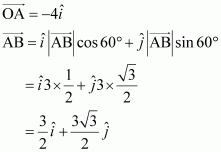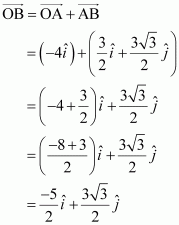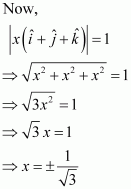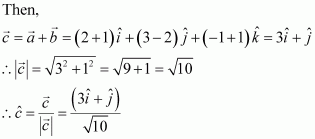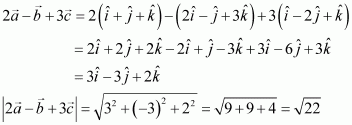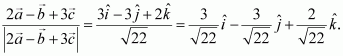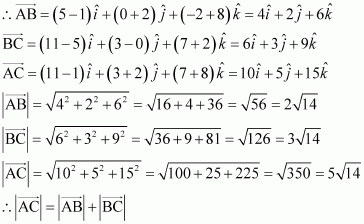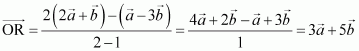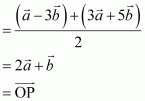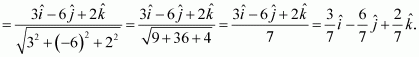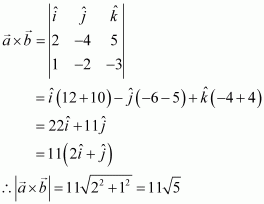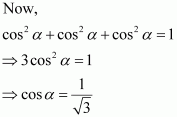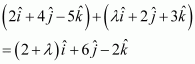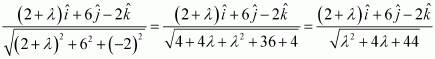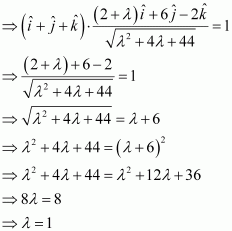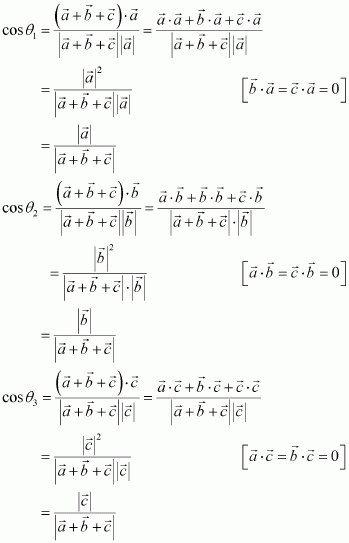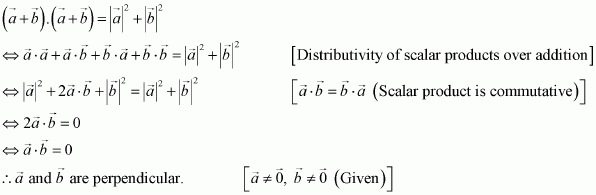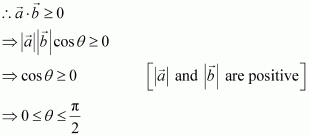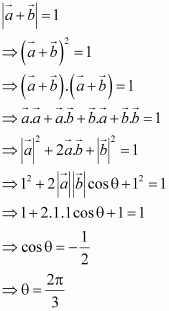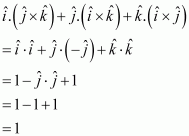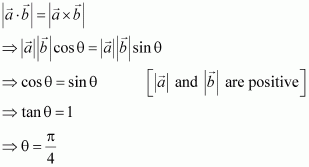Page No 428:
Question 1:
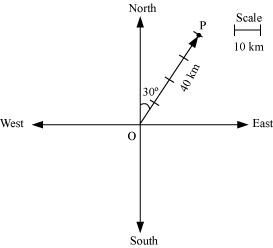
Represent graphically a displacement of 40 km, 30° east of north.
Answer:
Here, vector represents the displacement of 40 km, 30° East of North.
Question 2:
Classify the following measures as scalars and vectors.
(i) 10 kg (ii) 2 metres north-west (iii) 40°
(iv) 40 watt (v) 10–19 coulomb (vi) 20 m/s2
Answer:
(i) 10 kg is a scalar quantity because it involves only magnitude.
(ii) 2 meters north-west is a vector quantity as it involves both magnitude and direction.
(iii) 40° is a scalar quantity as it involves only magnitude.
(iv) 40 watts is a scalar quantity as it involves only magnitude.
(v) 10–19 coulomb is a scalar quantity as it involves only magnitude.
(vi) 20 m/s2 is a vector quantity as it involves magnitude as well as direction.
Question 3:
Classify the following as scalar and vector quantities.
(i) time period (ii) distance (iii) force
(iv) velocity (v) work done
Answer:
(i) Time period is a scalar quantity as it involves only magnitude.
(ii) Distance is a scalar quantity as it involves only magnitude.
(iii) Force is a vector quantity as it involves both magnitude and direction.
(iv) Velocity is a vector quantity as it involves both magnitude as well as direction.
(v) Work done is a scalar quantity as it involves only magnitude.
Question 4:
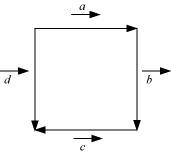
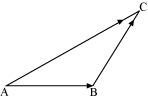
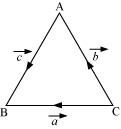
In Figure, identify the following vectors.
(i) Coinitial (ii) Equal (iii) Collinear but not equal
Answer:
(i) Vectors and
are coinitial because they have the same initial point.
(ii) Vectorsand
are equal because they have the same magnitude and direction.
(iii) Vectorsand
are collinear but not equal. This is because although they are parallel, their directions are not the same.
Question 5:
Answer the following as true or false.
(i) and
are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
Answer:
(i) True.
Vectors and
are parallel to the same line.
(ii) False.
Collinear vectors are those vectors that are parallel to the same line.
(iii) False.
It is not necessary for two vectors having the same magnitude to be parallel to the same line.
(iv) False.
Two vectors are said to be equal if they have the same magnitude and direction, regardless of the positions of their initial points.
Page No 440:
Question 1:
Compute the magnitude of the following vectors:
Answer:
The given vectors are:
Question 2:
Write two different vectors having same magnitude.
Answer:
Hence, are two different vectors having the same magnitude. The vectors are different because they have different directions.
Question 3:
Write two different vectors having same direction.
Answer:
The direction cosines of are the same. Hence, the two vectors have the same direction.
Question 4:
Find the values of x and y so that the vectors are equal
Answer:
The two vectors will be equal if their corresponding components are equal.
Hence, the required values of x and y are 2 and 3 respectively.
Question 5:
Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (–5, 7).
Answer:
The vector with the initial point P (2, 1) and terminal point Q (–5, 7) can be given by,
Hence, the required scalar components are –7 and 6 while the vector components are
Question 6:
Find the sum of the vectors.
Answer:
The given vectors are.
Question 7:
Find the unit vector in the direction of the vector.
Answer:
The unit vector in the direction of vector
is given by
.
Question 8:
Find the unit vector in the direction of vector, where P and Q are the points
(1, 2, 3) and (4, 5, 6), respectively.
Answer:
The given points are P (1, 2, 3) and Q (4, 5, 6).
Hence, the unit vector in the direction of is
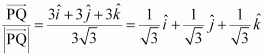
Question 9:
For given vectors, and
, find the unit vector in the direction of the vector
Answer:
The given vectors are and
.
Hence, the unit vector in the direction of is
a→+b→a→+b→=i^+k^2=12i⏜+12k⏜.
Question 10:
Find a vector in the direction of vector which has magnitude 8 units.
Answer:
Hence, the vector in the direction of vector which has magnitude 8 units is given by,
Question 11:
Show that the vectorsare collinear.
Answer:
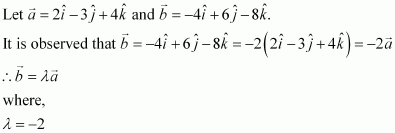
Hence, the given vectors are collinear.
Question 12:
Find the direction cosines of the vector
Answer:
Hence, the direction cosines of
Question 13:
Find the direction cosines of the vector joining the points A (1, 2, –3) and
B (–1, –2, 1) directed from A to B.
Answer:
The given points are A (1, 2, –3) and B (–1, –2, 1).
Hence, the direction cosines of are
Question 14:
Show that the vector is equally inclined to the axes OX, OY, and OZ.
Answer:
Therefore, the direction cosines of
Now, let α, β, and γbe the angles formed by with the positive directions of x, y, and z axes.
Then, we have
Hence, the given vector is equally inclined to axes OX, OY, and OZ.
Question 15:
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are respectively, in the ration 2:1
(i) internally
(ii) externally
Answer:
The position vector of point R dividing the line segment joining two points
P and Q in the ratio m: n is given by:
- Internally:
- Externally:
Position vectors of P and Q are given as:
(i) The position vector of point R which divides the line joining two points P and Q internally in the ratio 2:1 is given by,
(ii) The position vector of point R which divides the line joining two points P and Q externally in the ratio 2:1 is given by,
Page No 441:
Question 16:
Find the position vector of the mid point of the vector joining the points P (2, 3, 4) and Q (4, 1, – 2).
Answer:
The position vector of mid-point R of the vector joining points P (2, 3, 4) and Q (4, 1, – 2) is given by,
Question 17:
Show that the points A, B and C with position vectors,,
respectively form the vertices of a right angled triangle.
Answer:
Position vectors of points A, B, and C are respectively given as:
AB→2+CA→2=35+6=41=BC→2Hence, ABC is a right-angled triangle.
Question 18:
In triangle ABC which of the following is not true:
A.
B.
C.
D.
Answer:
On applying the triangle law of addition in the given triangle, we have:
From equations (1) and (3), we have:
Hence, the equation given in alternative C is incorrect.
The correct answer is C.
Question 19:
If are two collinear vectors, then which of the following are incorrect:
A. , for some scalar λ
B.
C. the respective components of are proportional
D. both the vectors have same direction, but different magnitudes
Answer:
If are two collinear vectors, then they are parallel.
Therefore, we have:
(For some scalar λ)
If λ = ±1, then .
Thus, the respective components of are proportional.
However, vectors can have different directions.
Hence, the statement given in D is incorrect.
The correct answer is D.
Page No 447:
Question 1:
Find the angle between two vectorsand
with magnitudes
and 2, respectively having
.
Answer:
It is given that,
Now, we know that.
Hence, the angle between the given vectors and
is
.
Question 2:
Find the angle between the vectors
Answer:
The given vectors are.
Also, we know that.
Question 3:
Find the projection of the vectoron the vector
.
Answer:
Letand
.
Now, projection of vectoron
is given by,
Hence, the projection of vector on
is 0.
Question 4:
Find the projection of the vectoron the vector
.
Answer:
Letand
.
Now, projection of vectoron
is given by,
Question 5:
Show that each of the given three vectors is a unit vector:
Also, show that they are mutually perpendicular to each other.
Answer:
Thus, each of the given three vectors is a unit vector.
Hence, the given three vectors are mutually perpendicular to each other.
Page No 448:
Question 6:
Findand
, if
.
Answer:
Question 7:
Evaluate the product.
Answer:
Question 8:
Find the magnitude of two vectors, having the same magnitude and such that the angle between them is 60° and their scalar product is
.
Answer:
Let θ be the angle between the vectors
It is given that
We know that.
Question 9:
Find, if for a unit vector
.
Answer:
Question 10:
Ifare such that
is perpendicular to
, then find the value of λ.
Answer:
Hence, the required value of λ is 8.
Question 11:
Show that is perpendicular to
, for any two nonzero vectors
Answer:
Hence, and
are perpendicular to each other.
Question 12:
If, then what can be concluded about the vector
?
Answer:
It is given that.
Hence, vectorsatisfying
can be any vector.
Question 13:
If are unit vectors such that
, find the value of
.
Answer:
It is given that .
From (1), (2) and (3),
Question 14:
If either vector, then
. But the converse need not be true. Justify your answer with an example.
Answer:
We now observe that:
Hence, the converse of the given statement need not be true.
Question 15:
If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find ∠ABC. [∠ABC is the angle between the vectorsand
]
Answer:
The vertices of ΔABC are given as A (1, 2, 3), B (–1, 0, 0), and C (0, 1, 2).
Also, it is given that ∠ABC is the angle between the vectorsand
.
Now, it is known that:
.
Question 16:
Show that the points A (1, 2, 7), B (2, 6, 3) and C (3, 10, –1) are collinear.
Answer:
The given points are A (1, 2, 7), B (2, 6, 3), and C (3, 10, –1).
Hence, the given points A, B, and C are collinear.
Question 17:
Show that the vectorsform the vertices of a right angled triangle.
Answer:
Let vectors be position vectors of points A, B, and C respectively.
Now, vectorsrepresent the sides of ΔABC.
Hence, ΔABC is a right-angled triangle.
Question 18:
Ifis a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then λ
is unit vector if
(A) λ = 1 (B) λ = –1 (C)
(D)
Answer:
Vectoris a unit vector if
.
Hence, vectoris a unit vector if
.
The correct answer is D.
Page No 454:
Question 1:
Find, if
and
.
Answer:
We have,
and
Question 2:
Find a unit vector perpendicular to each of the vector and
, where
and
.
Answer:
We have,
and
Hence, the unit vector perpendicular to each of the vectors and
is given by the relation,
Question 3:
If a unit vector makes an angles
with
with
and an acute angle θ with
, then find θ and hence, the compounds of
.
Answer:
Let unit vector have (a1, a2, a3) components.
⇒
Since is a unit vector,
.
Also, it is given that makes angles
with
with
, and an acute angle θ with
Then, we have:
Hence, and the components of
are
.
Question 4:
Show that
Answer:
Question 5:
Find λ and μ if .
Answer:
On comparing the corresponding components, we have:
Hence,
Question 6:
Given that and
. What can you conclude about the vectors
?
Answer:
Then,
(i) Either or
, or
(ii) Either or
, or
But, and
cannot be perpendicular and parallel simultaneously.
Hence, or
.
Question 7:
Let the vectors given as
. Then show that
Answer:
We have,
On adding (2) and (3), we get:
Now, from (1) and (4), we have:
Hence, the given result is proved.
Question 8:
If either or
, then
. Is the converse true? Justify your answer with an example.
Answer:
Take any parallel non-zero vectors so that.
It can now be observed that:
Hence, the converse of the given statement need not be true.
Question 9:
Find the area of the triangle with vertices A (1, 1, 2), B (2, 3, 5) and
C (1, 5, 5).
Answer:
The vertices of triangle ABC are given as A (1, 1, 2), B (2, 3, 5), and
C (1, 5, 5).
The adjacent sidesand
of ΔABC are given as:
Area of ΔABC
Hence, the area of ΔABC
Page No 455:
Question 10:
Find the area of the parallelogram whose adjacent sides are determined by the vector .
Answer:
The area of the parallelogram whose adjacent sides are is
.
Adjacent sides are given as:
Hence, the area of the given parallelogram is.
Question 11:
Let the vectors and
be such that
and
, then
is a unit vector, if the angle between
and
is
(A) (B)
(C)
(D)
Answer:
It is given that.
We know that, where
is a unit vector perpendicular to both
and
and θ is the angle between
and
.
Now, is a unit vector if
.
Hence, is a unit vector if the angle between
and
is
.
The correct answer is B.
Question 12:
Area of a rectangle having vertices A, B, C, and D with position vectors and
respectively is
(A) (B) 1
(C) 2 (D)
Answer:
The position vectors of vertices A, B, C, and D of rectangle ABCD are given as:
The adjacent sides and
of the given rectangle are given as:
⇒AB→×BC→=2Now, it is known that the area of a parallelogram whose adjacent sides are is
.
Hence, the area of the given rectangle is
The correct answer is C.
Page No 458:
Question 1:
Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of x-axis.
Answer:
If is a unit vector in the XY-plane, then
Here, θ is the angle made by the unit vector with the positive direction of the x-axis.
Therefore, for θ = 30°:
Hence, the required unit vector is.
Question 2:
Find the scalar components and magnitude of the vector joining the points
.
Answer:
The vector joining the pointscan be obtained by,
Hence, the scalar components and the magnitude of the vector joining the given points are respectively and
.
Question 3:
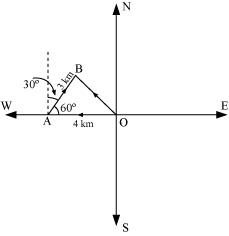
A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.
Answer:
Let O and B be the initial and final positions of the girl respectively.
Then, the girl’s position can be shown as:
Now, we have:
By the triangle law of vector addition, we have:
Hence, the girl’s displacement from her initial point of departure is
.
Question 4:
If, then is it true that
? Justify your answer.
Answer:
Now, by the triangle law of vector addition, we have.
It is clearly known that represent the sides of ΔABC.
Also, it is known that the sum of the lengths of any two sides of a triangle is greater than the third side.
Hence, it is not true that.
Question 5:
Find the value of x for whichis a unit vector.
Answer:
is a unit vector if
.
Hence, the required value of x is.
Question 6:
Find a vector of magnitude 5 units, and parallel to the resultant of the vectors
.
Answer:
We have,
Letbe the resultant of
.
Hence, the vector of magnitude 5 units and parallel to the resultant of vectors is
Question 7:
If, find a unit vector parallel to the vector
.
Answer:
We have,
Hence, the unit vector alongis
Question 8:
Show that the points A (1, –2, –8), B (5, 0, –2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.
Answer:
The given points are A (1, –2, –8), B (5, 0, –2), and C (11, 3, 7).
Thus, the given points A, B, and C are collinear.
Now, let point B divide AC in the ratio. Then, we have:
On equating the corresponding components, we get:
Hence, point B divides AC in the ratio
Question 9:
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors areexternally in the ratio 1: 2. Also, show that P is the mid point of the line segment RQ.
Answer:
It is given that.
It is given that point R divides a line segment joining two points P and Q externally in the ratio 1: 2. Then, on using the section formula, we get:
Therefore, the position vector of point R is.
Position vector of the mid-point of RQ =
Hence, P is the mid-point of the line segment RQ.
Question 10:
The two adjacent sides of a parallelogram areand
.
Find the unit vector parallel to its diagonal. Also, find its area.
Answer:
Adjacent sides of a parallelogram are given as: and
Then, the diagonal of a parallelogram is given by.
Thus, the unit vector parallel to the diagonal is
Area of parallelogram ABCD =
Hence, the area of the parallelogram issquare units.
Question 11:
Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are.
Answer:
Let a vector be equally inclined to axes OX, OY, and OZ at angle α.
Then, the direction cosines of the vector are cos α, cos α, and cos α.
Hence, the direction cosines of the vector which are equally inclined to the axes are.
Question 12:
Let and
. Find a vector
which is perpendicular to both
and
, and
.
Answer:
Let.
Sinceis perpendicular to both
and
, we have:
Also, it is given that:
On solving (i), (ii), and (iii), we get:
Hence, the required vector is.
Question 13:
The scalar product of the vectorwith a unit vector along the sum of vectors
and
is equal to one. Find the value of
.
Answer:
Therefore, unit vector alongis given as:
Scalar product ofwith this unit vector is 1.
Hence, the value of λ is 1.
Question 14:
If are mutually perpendicular vectors of equal magnitudes, show that the vector
is equally inclined to
and
.
Answer:
Sinceare mutually perpendicular vectors, we have
It is given that:
Let vector be inclined to
at angles
respectively.
Then, we have:
Now, as,
.
Hence, the vectoris equally inclined to
.
Page No 459:
Question 15:
Prove that, if and only if
are perpendicular, given
.
Answer:
Question 16:
If θ is the angle between two vectors and
, then
only when
(A) (B)
(C) (D)
Answer:
Let θ be the angle between two vectors and
.
Then, without loss of generality, and
are non-zero vectors so that
.
It is known that.
Hence, when
.
The correct answer is B.
Question 17:
Let and
be two unit vectors andθ is the angle between them. Then
is a unit vector if
(A) (B)
(C)
(D)
Answer:
Let and
be two unit vectors andθ be the angle between them.
Then, .
Now, is a unit vector if
.
Hence, is a unit vector if
.
The correct answer is D.
Question 18:
The value of is
(A) 0 (B) –1 (C) 1 (D) 3
Answer:
The correct answer is C.
Question 19:
If θ is the angle between any two vectors and
, then
when θisequal to
(A) 0 (B) (C)
(D) π
Answer:
Let θ be the angle between two vectors and
.
Then, without loss of generality, and
are non-zero vectors, so that
.
Hence, when θisequal to
.
The correct answer is B.