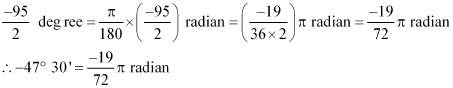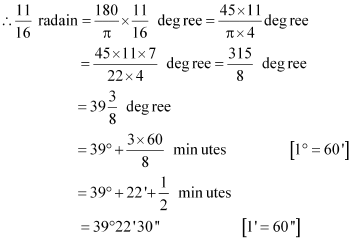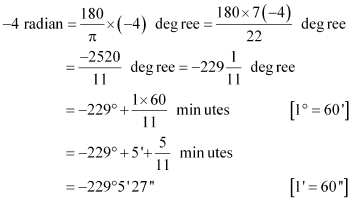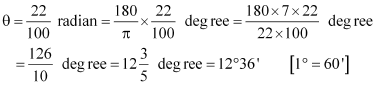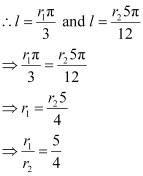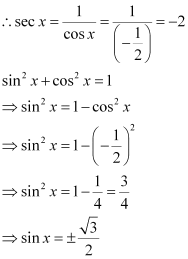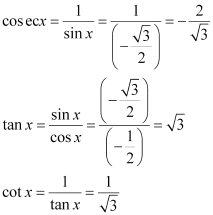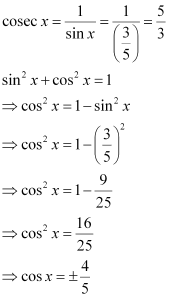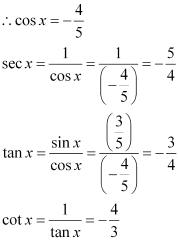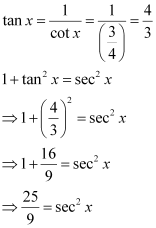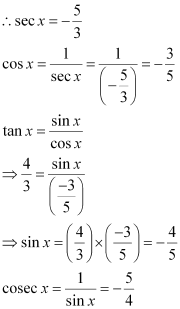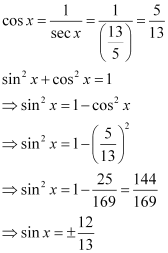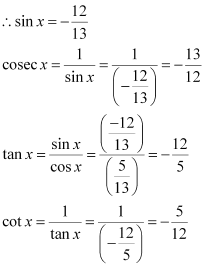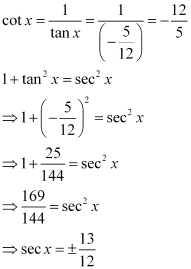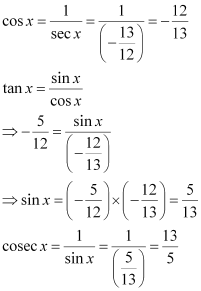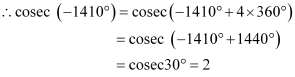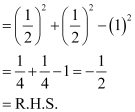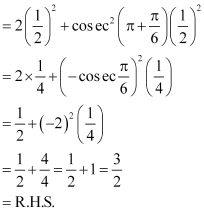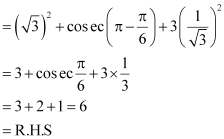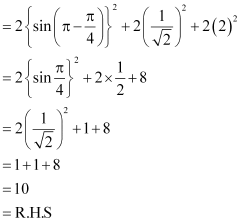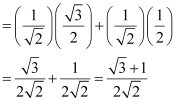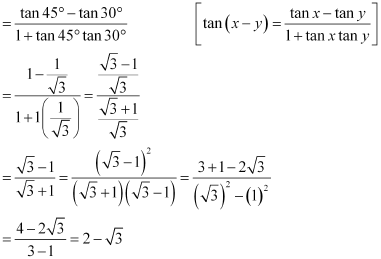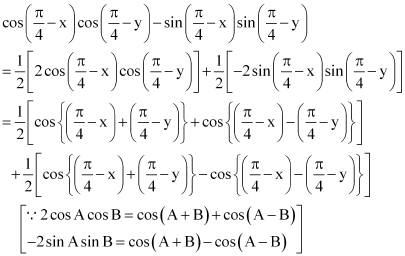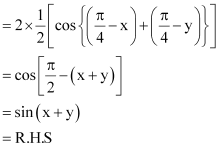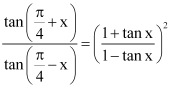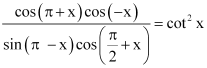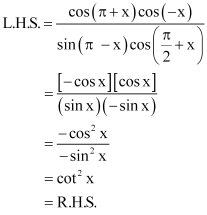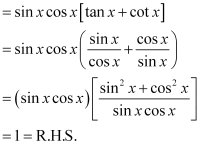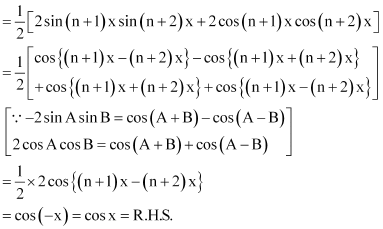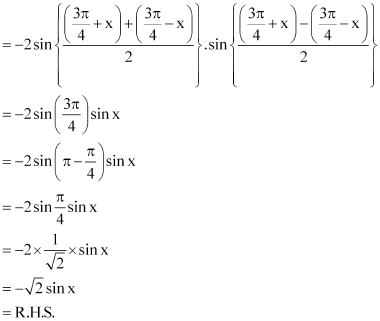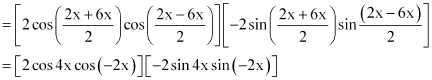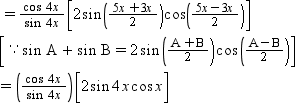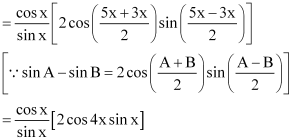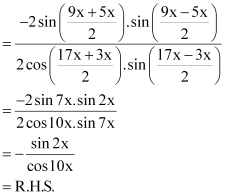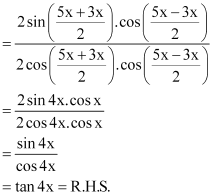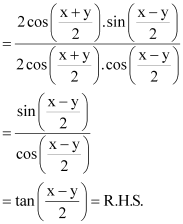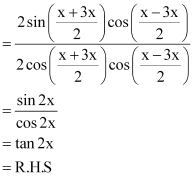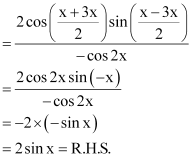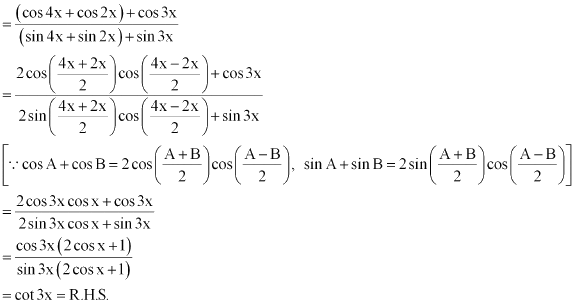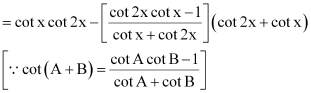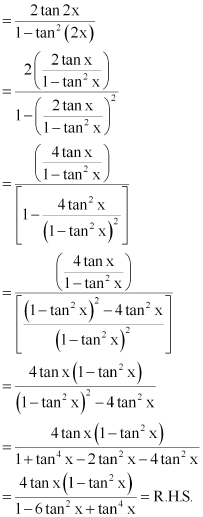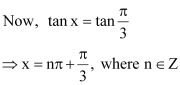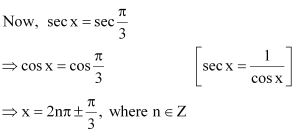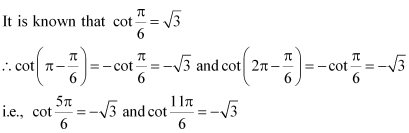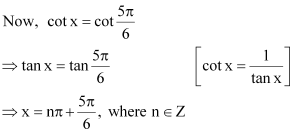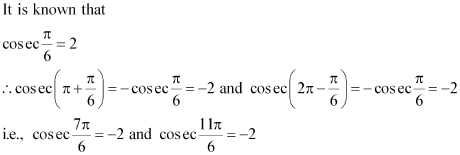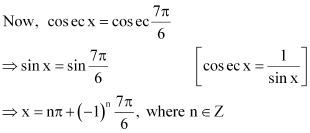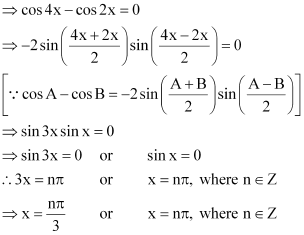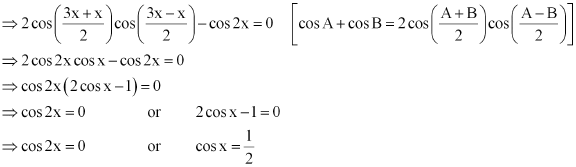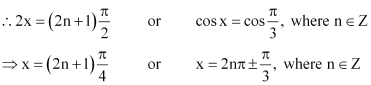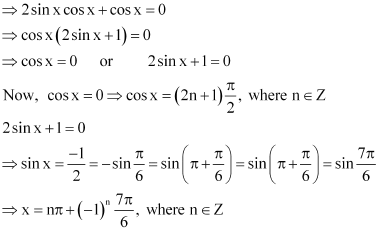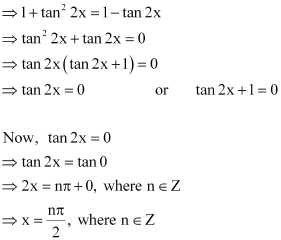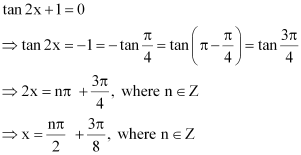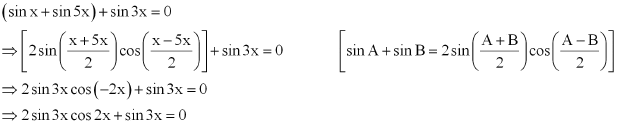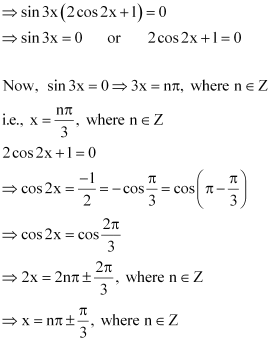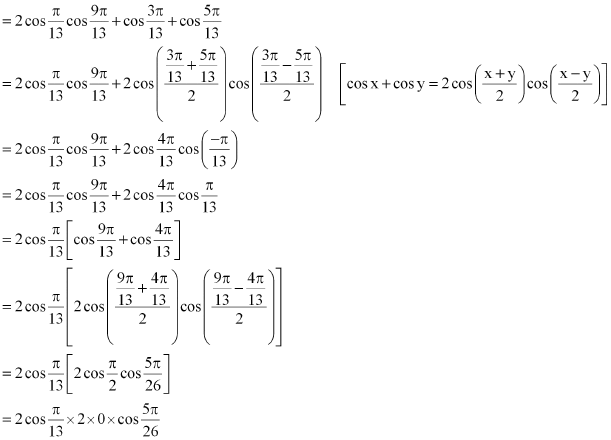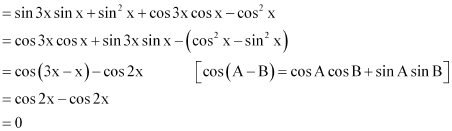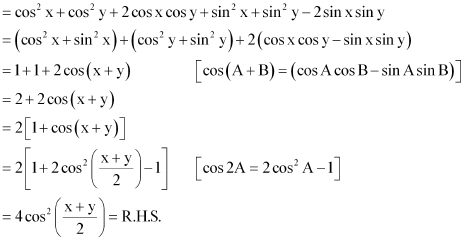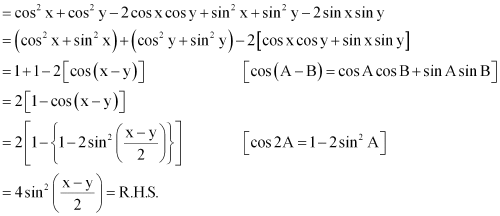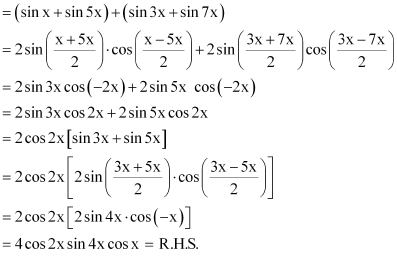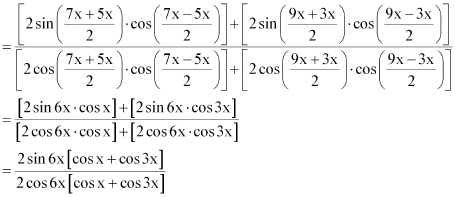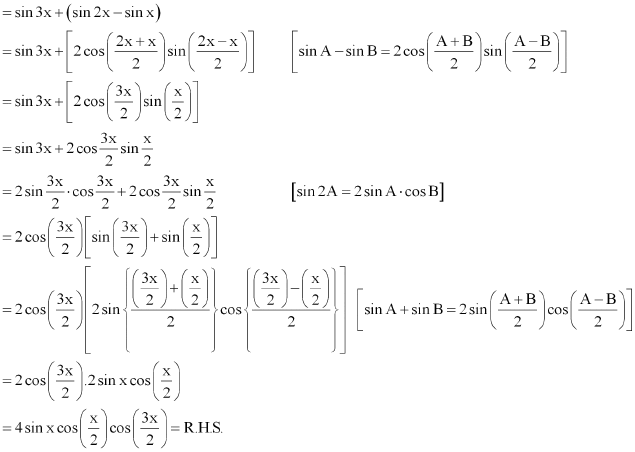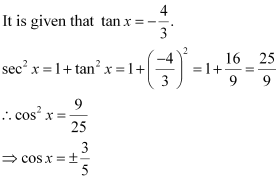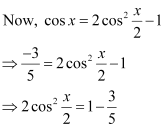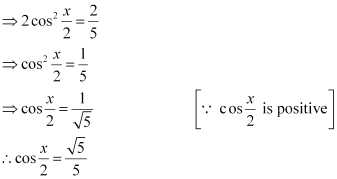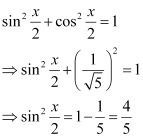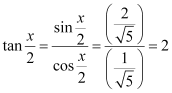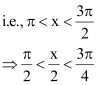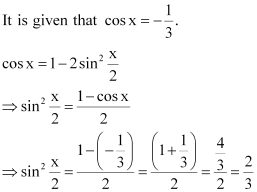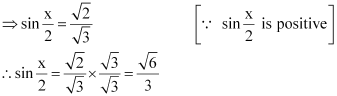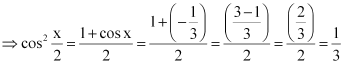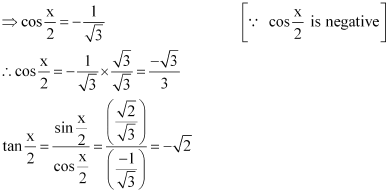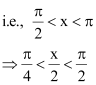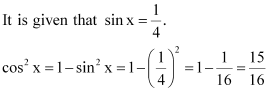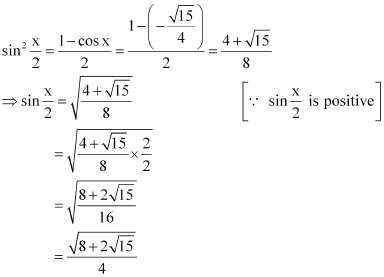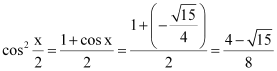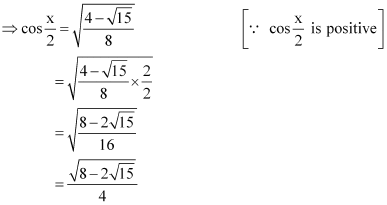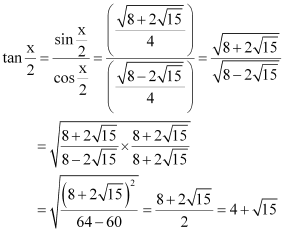NCERT Solutions for Class 11 Maths Chapter 3 – Trigonometric Functions
Page No 54:
Question 1:
Find the radian measures corresponding to the following degree measures:
(i) 25° (ii) – 47° 30′ (iii) 240° (iv) 520°
ANSWER:
(i) 25°
We know that 180° = π radian
(ii) –47° 30′
–47° 30′ = degree [1° = 60′]
degree
Since 180° = π radian
(iii) 240°
We know that 180° = π radian
(iv) 520°
We know that 180° = π radian
Page No 55:
Question 2:
Find the degree measures corresponding to the following radian measures
.
(i) (ii) – 4 (iii)
(iv)
ANSWER:
(i)
We know that π radian = 180°
(ii) – 4
We know that π radian = 180°
(iii)
We know that π radian = 180°
(iv)
We know that π radian = 180°
Page No 55:
Question 3:
A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
ANSWER:
Number of revolutions made by the wheel in 1 minute = 360
∴Number of revolutions made by the wheel in 1 second =
In one complete revolution, the wheel turns an angle of 2π radian.
Hence, in 6 complete revolutions, it will turn an angle of 6 × 2π radian, i.e.,
12 π radian
Thus, in one second, the wheel turns an angle of 12π radian.
Page No 55:
Question 4:
Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm.
ANSWER:
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then
Therefore, forr = 100 cm, l = 22 cm, we have
Thus, the required angle is 12°36′.
Page No 55:
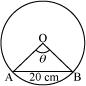
Question 5:
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
ANSWER:
Diameter of the circle = 40 cm
∴Radius (r) of the circle =
Let AB be a chord (length = 20 cm) of the circle.
In ΔOAB, OA = OB = Radius of circle = 20 cm
Also, AB = 20 cm
Thus, ΔOAB is an equilateral triangle.
∴θ = 60° =
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then.
Thus, the length of the minor arc of the chord is.
Page No 55:
Question 6:
If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
ANSWER:
Let the radii of the two circles be and
. Let an arc of length l subtend an angle of 60° at the centre of the circle of radius r1, while let an arc of length l subtend an angle of 75° at the centre of the circle of radius r2.
Now, 60° =and 75° =
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then.
Thus, the ratio of the radii is 5:4.
Page No 55:
Question 7:
Find the angle in radian though which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm (ii) 15 cm (iii) 21 cm
ANSWER:
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then.
It is given that r = 75 cm
(i) Here, l = 10 cm
(ii) Here, l = 15 cm
(iii) Here, l = 21 cm
Page No 63:
Question 1:
Find the values of other five trigonometric functions if , x lies in third quadrant.
ANSWER:
Since x lies in the 3rd quadrant, the value of sin x will be negative.
Page No 63:
Question 2:
Find the values of other five trigonometric functions if , x lies in second quadrant.
ANSWER:
Since x lies in the 2nd quadrant, the value of cos x will be negative
Page No 63:
Question 3:
Find the values of other five trigonometric functions if , x lies in third quadrant.
ANSWER:
Since x lies in the 3rd quadrant, the value of sec x will be negative.
Page No 63:
Question 4:
Find the values of other five trigonometric functions if , x lies in fourth quadrant.
ANSWER:
Since x lies in the 4th quadrant, the value of sin x will be negative.
Page No 63:
Question 5:
Find the values of other five trigonometric functions if , x lies in second quadrant.
ANSWER:
Since x lies in the 2nd quadrant, the value of sec x will be negative.
∴sec x =
Page No 63:
Question 6:
Find the value of the trigonometric function sin 765°
ANSWER:
It is known that the values of sin x repeat after an interval of 2π or 360°.
Page No 63:
Question 7:
Find the value of the trigonometric function cosec (–1410°)
ANSWER:
It is known that the values of cosec x repeat after an interval of 2π or 360°.
Page No 63:
Question 8:
Find the value of the trigonometric function
ANSWER:
It is known that the values of tan x repeat after an interval of π or 180°.
Page No 63:
Question 9:
Find the value of the trigonometric function
ANSWER:
It is known that the values of sin x repeat after an interval of 2π or 360°.
Page No 63:
Question 10:
Find the value of the trigonometric function
ANSWER:
It is known that the values of cot x repeat after an interval of π or 180°.
Page No 73:
Question 1:
ANSWER:
L.H.S. =
Page No 73:
Question 2:
Prove that
ANSWER:
L.H.S. =
Page No 73:
Question 3:
Prove that
ANSWER:
L.H.S. =
Page No 73:
Question 4:
Prove that
ANSWER:
L.H.S =
Page No 73:
Question 5:
Find the value of:
(i) sin 75°
(ii) tan 15°
ANSWER:
(i) sin 75° = sin (45° + 30°)
= sin 45° cos 30° + cos 45° sin 30°
[sin (x + y) = sin x cos y + cos x sin y]
(ii) tan 15° = tan (45° – 30°)
Page No 73:
Question 6:
Prove that:
ANSWER:
Page No 73:
Question 7:
Prove that:
ANSWER:
It is known that
∴L.H.S. =
Page No 73:
Question 8:
Prove that
ANSWER:
Page No 73:
Question 9:
ANSWER:
L.H.S. =
Page No 73:
Question 10:
Prove that sin (n + 1)x sin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x
ANSWER:
L.H.S. = sin (n + 1)x sin(n + 2)x + cos (n + 1)x cos(n + 2)x
Page No 73:
Question 11:
Prove that
ANSWER:
It is known that.
∴L.H.S. =
Page No 73:
Question 12:
Prove that sin2 6x – sin2 4x = sin 2x sin 10x
ANSWER:
It is known that
∴L.H.S. = sin26x – sin24x
= (sin 6x + sin 4x) (sin 6x – sin 4x)
= (2 sin 5x cos x) (2 cos 5x sin x)
= (2 sin 5x cos 5x) (2 sin x cos x)
= sin 10x sin 2x
= R.H.S.
Page No 73:
Question 13:
Prove that cos2 2x – cos2 6x = sin 4x sin 8x
ANSWER:
It is known that
∴L.H.S. = cos2 2x – cos2 6x
= (cos 2x + cos 6x) (cos 2x – 6x)
= [2 cos 4x cos 2x] [–2 sin 4x (–sin 2x)]
= (2 sin 4x cos 4x) (2 sin 2x cos 2x)
= sin 8x sin 4x
= R.H.S.
Page No 73:
Question 14:
Prove that sin 2x + 2sin 4x + sin 6x = 4cos2 x sin 4x
ANSWER:
L.H.S. = sin 2x + 2 sin 4x + sin 6x
= [sin 2x + sin 6x] + 2 sin 4x
= 2 sin 4x cos (– 2x) + 2 sin 4x
= 2 sin 4x cos 2x + 2 sin 4x
= 2 sin 4x (cos 2x + 1)
= 2 sin 4x (2 cos2 x – 1 + 1)
= 2 sin 4x (2 cos2 x)
= 4cos2 x sin 4x
= R.H.S.
Page No 73:
Question 15:
Prove that cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
ANSWER:
L.H.S = cot 4x (sin 5x + sin 3x)
= 2 cos 4x cos x
R.H.S. = cot x (sin 5x – sin 3x)
= 2 cos 4x. cos x
L.H.S. = R.H.S.
Page No 73:
Question 16:
Prove that
ANSWER:
It is known that
∴L.H.S =
Page No 73:
Question 17:
Prove that
ANSWER:
It is known that
∴L.H.S. =
Page No 73:
Question 18:
Prove that
ANSWER:
It is known that
∴L.H.S. =
Page No 73:
Question 19:
Prove that
ANSWER:
It is known that
∴L.H.S. =
Page No 73:
Question 20:
Prove that
ANSWER:
It is known that
∴L.H.S. =
Page No 73:
Question 21:
Prove that
ANSWER:
L.H.S. =
Page No 74:
Question 22:
Prove that cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1
ANSWER:
L.H.S. = cot x cot 2x – cot 2x cot 3x – cot 3x cot x
= cot x cot 2x – cot 3x (cot 2x + cot x)
= cot x cot 2x – cot (2x + x) (cot 2x + cot x)
= cot x cot 2x – (cot 2x cot x – 1)
= 1 = R.H.S.
Page No 74:
Question 23:
Prove that
ANSWER:
It is known that.
∴L.H.S. = tan 4x = tan 2(2x)
Page No 74:
Question 24:
Prove that cos 4x = 1 – 8sin2 x cos2 x
ANSWER:
L.H.S. = cos 4x
= cos 2(2x)
= 1 – 2 sin2 2x [cos 2A = 1 – 2 sin2 A]
= 1 – 2(2 sin x cos x)2 [sin2A = 2sin A cosA]
= 1 – 8 sin2x cos2x
= R.H.S.
Page No 74:
Question 25:
Prove that: cos 6x = 32 cos6 x – 48 cos4 x + 18 cos2 x – 1
ANSWER:
L.H.S. = cos 6x
= cos 3(2x)
= 4 cos3 2x – 3 cos 2x [cos 3A = 4 cos3 A – 3 cos A]
= 4 [(2 cos2 x – 1)3 – 3 (2 cos2 x – 1) [cos 2x = 2 cos2 x – 1]
= 4 [(2 cos2 x)3 – (1)3 – 3 (2 cos2 x)2 + 3 (2 cos2 x)] – 6cos2 x + 3
= 4 [8cos6x – 1 – 12 cos4x + 6 cos2x] – 6 cos2x + 3
= 32 cos6x – 4 – 48 cos4x + 24 cos2 x – 6 cos2x + 3
= 32 cos6x – 48 cos4x + 18 cos2x – 1
= R.H.S.
Page No 78:
Question 1:
Find the principal and general solutions of the equation
ANSWER:
Therefore, the principal solutions are x =and
.
Therefore, the general solution is
Page No 78:
Question 2:
Find the principal and general solutions of the equation
ANSWER:
Therefore, the principal solutions are x =and
.
Therefore, the general solution is, where n ∈ Z
Page No 78:
Question 3:
Find the principal and general solutions of the equation
ANSWER:
Therefore, the principal solutions are x = and
.
Therefore, the general solution is
Page No 78:
Question 4:
Find the general solution of cosec x = –2
ANSWER:
cosec x = –2
Therefore, the principal solutions are x =.
Therefore, the general solution is
Page No 78:
Question 5:
Find the general solution of the equation
ANSWER:
Page No 78:
Question 6:
Find the general solution of the equation
ANSWER:
Page No 78:
Question 7:
Find the general solution of the equation
ANSWER:
Therefore, the general solution is.
Page No 78:
Question 8:
Find the general solution of the equation
ANSWER:
Therefore, the general solution is.
Page No 78:
Question 9:
Find the general solution of the equation
ANSWER:
Therefore, the general solution is
Page No 81:
Question 1:
Prove that:
ANSWER:
L.H.S.
= 0 = R.H.S
Page No 81:
Question 2:
Prove that: (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0
ANSWER:
L.H.S.
= (sin 3x + sin x) sin x + (cos 3x – cos x) cos x
= RH.S.
Page No 82:
Question 3:
Prove that:
ANSWER:
L.H.S. =
Page No 82:
Question 4:
Prove that:
ANSWER:
L.H.S. =
Page No 82:
Question 5:
Prove that:
ANSWER:
It is known that.
∴L.H.S. =
Page No 82:
Question 6:
Prove that:
ANSWER:
It is known that
.
L.H.S. =
= tan 6x
= R.H.S.
Page No 82:
Question 7:
Prove that:
ANSWER:
L.H.S. =
Page No 82:
Question 8:
, x in quadrant II
ANSWER:
Here, x is in quadrant II.
i.e.,
Therefore, are all positive.
As x is in quadrant II, cosx is negative.
∴
Thus, the respective values of are
.
Page No 82:
Question 9:
Find for
, x in quadrant III
ANSWER:
Here, x is in quadrant III.
Therefore, and
are negative, whereas
is positive.
Now,
Thus, the respective values of are
.
Page No 82:
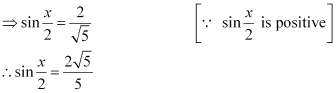
Question 10:
Find for
, x in quadrant II
ANSWER:
Here, x is in quadrant II.
Therefore,, and
are all positive.
[cosx is negative in quadrant II]
Thus, the respective values of are
.