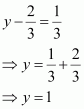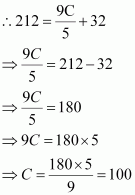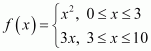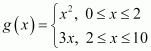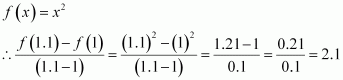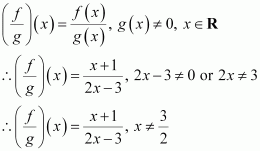NCERT Solutions for Class 11 Maths Chapter 2 – Relations and Functions
Page No 33:
Question 1:
If, find the values of x and y.
ANSWER:
It is given that.
Since the ordered pairs are equal, the corresponding elements will also be equal.
Therefore, and
.
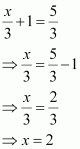
∴ x = 2 and y = 1
Page No 33:
Question 2:
If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A × B)?
ANSWER:
It is given that set A has 3 elements and the elements of set B are 3, 4, and 5.
⇒ Number of elements in set B = 3
Number of elements in (A × B)
= (Number of elements in A) × (Number of elements in B)
= 3 × 3 = 9
Thus, the number of elements in (A × B) is 9.
Page No 33:
Question 3:
If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.
ANSWER:
G = {7, 8} and H = {5, 4, 2}
We know that the Cartesian product P × Q of two non-empty sets P and Q is defined as
P × Q = {(p, q): p∈ P, q ∈ Q}
∴G × H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
H × G = {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}
Page No 33:
Question 4:
State whether each of the following statement are true or false. If the statement is false, rewrite the given statement correctly.
(i) If P = {m, n} and Q = {n, m}, then P × Q = {(m, n), (n, m)}.
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ Φ) = Φ.
ANSWER:
(i) False
If P = {m, n} and Q = {n, m}, then
P × Q = {(m, m), (m, n), (n, m), (n, n)}
(ii) True
(iii) True
Page No 33:
Question 5:
If A = {–1, 1}, find A × A × A.
ANSWER:
It is known that for any non-empty set A, A × A × A is defined as
A × A × A = {(a, b, c): a, b, c ∈ A}
It is given that A = {–1, 1}
∴ A × A × A = {(–1, –1, –1), (–1, –1, 1), (–1, 1, –1), (–1, 1, 1),
(1, –1, –1), (1, –1, 1), (1, 1, –1), (1, 1, 1)}
Page No 33:
Question 6:
If A × B = {(a, x), (a, y), (b, x), (b, y)}. Find A and B.
ANSWER:
It is given that A × B = {(a, x), (a, y), (b, x), (b, y)}
We know that the Cartesian product of two non-empty sets P and Q is defined as P × Q = {(p, q): p ∈ P, q ∈ Q}
∴ A is the set of all first elements and B is the set of all second elements.
Thus, A = {a, b} and B = {x, y}
Page No 33:
Question 7:
Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) A × C is a subset of B × D
ANSWER:
(i) To verify: A × (B ∩ C) = (A × B) ∩ (A × C)
We have B ∩ C = {1, 2, 3, 4} ∩ {5, 6} = Φ
∴L.H.S. = A × (B ∩ C) = A × Φ = Φ
A × B = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
∴ R.H.S. = (A × B) ∩ (A × C) = Φ
∴L.H.S. = R.H.S
Hence, A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) To verify: A × C is a subset of B × D
A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
B × D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
We can observe that all the elements of set A × C are the elements of set B × D.
Therefore, A × C is a subset of B × D.
Page No 33:
Question 8:
Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.
ANSWER:
A = {1, 2} and B = {3, 4}
∴A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}
⇒ n(A × B) = 4
We know that if C is a set with n(C) = m, then n[P(C)] = 2m.
Therefore, the set A × B has 24 = 16 subsets. These are
Φ, {(1, 3)}, {(1, 4)}, {(2, 3)}, {(2, 4)}, {(1, 3), (1, 4)}, {(1, 3), (2, 3)},
{(1, 3), (2, 4)}, {(1, 4), (2, 3)}, {(1, 4), (2, 4)}, {(2, 3), (2, 4)},
{(1, 3), (1, 4), (2, 3)}, {(1, 3), (1, 4), (2, 4)}, {(1, 3), (2, 3), (2, 4)},
{(1, 4), (2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3), (2, 4)}
Page No 33:
Question 9:
Let A and B be two sets such that n(A) = 3 and n (B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.
ANSWER:
It is given that n(A) = 3 and n(B) = 2; and (x, 1), (y, 2), (z, 1) are in A × B.
We know that A = Set of first elements of the ordered pair elements of A × B
B = Set of second elements of the ordered pair elements of A × B.
∴ x, y, and z are the elements of A; and 1 and 2 are the elements of B.
Since n(A) = 3 and n(B) = 2, it is clear that A = {x, y, z} and B = {1, 2}.
Page No 34:
Question 10:
The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0, 1). Find the set A and the remaining elements of A × A.
ANSWER:
We know that if n(A) = p and n(B) = q, then n(A × B) = pq.
∴ n(A × A) = n(A) × n(A)
It is given that n(A × A) = 9
∴ n(A) × n(A) = 9
⇒ n(A) = 3
The ordered pairs (–1, 0) and (0, 1) are two of the nine elements of A × A.
We know that A × A = {(a, a): a ∈ A}. Therefore, –1, 0, and 1 are elements of A.
Since n(A) = 3, it is clear that A = {–1, 0, 1}.
The remaining elements of set A × A are (–1, –1), (–1, 1), (0, –1), (0, 0),
(1, –1), (1, 0), and (1, 1)
Page No 35:
Question 1:
Let A = {1, 2, 3, … , 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
ANSWER:
The relation R from A to A is given as
R = {(x, y): 3x – y = 0, where x, y ∈ A}
i.e., R = {(x, y): 3x = y, where x, y ∈ A}
∴R = {(1, 3), (2, 6), (3, 9), (4, 12)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
∴Domain of R = {1, 2, 3, 4}
The whole set A is the codomainof the relation R.
∴Codomain of R = A = {1, 2, 3, …, 14}
The range of R is the set of all second elements of the ordered pairs in the relation.
∴Range of R = {3, 6, 9, 12}
Page No 36:
Question 2:
Define a relation R on the set N of natural numbers by R = {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
ANSWER:
R = {(x, y): y = x + 5, x is a natural number less than 4, x, y ∈ N}
The natural numbers less than 4 are 1, 2, and 3.
∴R = {(1, 6), (2, 7), (3, 8)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
∴ Domain of R = {1, 2, 3}
The range of R is the set of all second elements of the ordered pairs in the relation.
∴ Range of R = {6, 7, 8}
Page No 36:
Question 3:
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.
ANSWER:
A = {1, 2, 3, 5} and B = {4, 6, 9}
R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}
∴R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}
Page No 36:
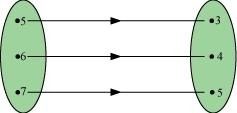
Question 4:
The given figure shows a relationship between the sets P and Q. write this relation
(i) in set-builder form (ii) in roster form.
What is its domain and range?
ANSWER:
According to the given figure, P = {5, 6, 7}, Q = {3, 4, 5}
(i) R = {(x, y): y = x – 2; x ∈ P} or R = {(x, y): y = x – 2 for x = 5, 6, 7}
(ii) R = {(5, 3), (6, 4), (7, 5)}
Domain of R = {5, 6, 7}
Range of R = {3, 4, 5}
Page No 36:
Question 5:
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by
{(a, b): a, b ∈ A, b is exactly divisible by a}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
ANSWER:
A = {1, 2, 3, 4, 6}, R = {(a, b): a, b ∈ A, b is exactly divisible by a}
(i) R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}
(ii) Domain of R = {1, 2, 3, 4, 6}
(iii) Range of R = {1, 2, 3, 4, 6}
Page No 36:
Question 6:
Determine the domain and range of the relation R defined by R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}.
ANSWER:
R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}
∴ R = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
∴Domain of R = {0, 1, 2, 3, 4, 5}
Range of R = {5, 6, 7, 8, 9, 10}
Page No 36:
Question 7:
Write the relation R = {(x, x3): x is a prime number less than 10} in roster form.
ANSWER:
R = {(x, x3): x is a prime number less than 10}
The prime numbers less than 10 are 2, 3, 5, and 7.
∴R = {(2, 8), (3, 27), (5, 125), (7, 343)}
Page No 36:
Question 8:
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
ANSWER:
It is given that A = {x, y, z} and B = {1, 2}.
∴ A × B = {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}
Since n(A × B) = 6, the number of subsets of A × B is 26.
Therefore, the number of relations from A to B is 26.
Page No 36:
Question 9:
Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
ANSWER:
R = {(a, b): a, b ∈ Z, a – b is an integer}
It is known that the difference between any two integers is always an integer.
∴Domain of R = Z
Range of R = Z
Page No 44:
Question 1:
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) {(1, 3), (1, 5), (2, 5)}
ANSWER:
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
Since 2, 5, 8, 11, 14, and 17 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 5, 8, 11, 14, 17} and range = {1}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Since 2, 4, 6, 8, 10, 12, and 14 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 4, 6, 8, 10, 12, 14} and range = {1, 2, 3, 4, 5, 6, 7}
(iii) {(1, 3), (1, 5), (2, 5)}
Since the same first element i.e., 1 corresponds to two different images i.e., 3 and 5, this relation is not a function.
Page No 44:
Question 2:
Find the domain and range of the following real function:
(i) f(x) = –|x| (ii)
ANSWER:
(i) f(x) = –|x|, x ∈ R
We know that |x| =
Since f(x) is defined for x ∈ R, the domain of f is R.
It can be observed that the range of f(x) = –|x| is all real numbers except positive real numbers.
∴The range of f is (–, 0].
(ii)
Sinceis defined for all real numbers that are greater than or equal to –3 and less than or equal to 3, the domain of f(x) is {x : –3 ≤ x ≤ 3} or [–3, 3].
For any value of x such that –3 ≤ x ≤ 3, the value of f(x) will lie between 0 and 3.
∴The range of f(x) is {x: 0 ≤ x ≤ 3} or [0, 3].
Page No 44:
Question 3:
A function f is defined by f(x) = 2x – 5. Write down the values of
(i) f(0), (ii) f(7), (iii) f(–3)
ANSWER:
The given function is f(x) = 2x – 5.
Therefore,
(i) f(0) = 2 × 0 – 5 = 0 – 5 = –5
(ii) f(7) = 2 × 7 – 5 = 14 – 5 = 9
(iii) f(–3) = 2 × (–3) – 5 = – 6 – 5 = –11
Page No 44:
Question 4:
The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by.
Find (i) t (0) (ii) t (28) (iii) t (–10) (iv) The value of C, when t(C) = 212
ANSWER:
The given function is.
Therefore,
(i)
(ii)
(iii)
(iv) It is given that t(C) = 212
Thus, the value of t, when t(C) = 212, is 100.
Page No 44:
Question 5:
Find the range of each of the following functions.
(i) f(x) = 2 – 3x, x ∈ R, x > 0.
(ii) f(x) = x2 + 2, x, is a real number.
(iii) f(x) = x, x is a real number
ANSWER:
(i) f(x) = 2 – 3x, x ∈ R, x > 0
The values of f(x) for various values of real numbers x > 0 can be written in the tabular form as
| x | 0.01 | 0.1 | 0.9 | 1 | 2 | 2.5 | 4 | 5 | … |
| f(x) | 1.97 | 1.7 | –0.7 | –1 | –4 | –5.5 | –10 | –13 | … |
Thus, it can be clearly observed that the range of f is the set of all real numbers less than 2.
i.e., range of f = (–, 2)
Alter:
Let x > 0
⇒ 3x > 0
⇒ 2 –3x < 2
⇒ f(x) < 2
∴Range of f = (–, 2)
(ii) f(x) = x2 + 2, x, is a real number
The values of f(x) for various values of real numbers x can be written in the tabular form as
| x | ±0.3 | ±0.8 | ±1 | ±2 | ±3 | … | ||
| f(x) | 2 | 2.09 | 2.64 | 3 | 6 | 11 | ….. |
Thus, it can be clearly observed that the range of f is the set of all real numbers greater than 2.
i.e., range of f = [2,)
Alter:
Let x be any real number.
Accordingly,
x2 ≥ 0
⇒ x2 + 2 ≥ 0 + 2
⇒ x2 + 2 ≥ 2
⇒ f(x) ≥ 2
∴ Range of f = [2,)
(iii) f(x) = x, x is a real number
It is clear that the range of f is the set of all real numbers.
∴ Range of f = R
Page No 46:
Question 1:
The relation f is defined by
The relation g is defined by
Show that f is a function and g is not a function.
ANSWER:
The relation f is defined as
It is observed that for
0 ≤ x < 3, f(x) = x2
3 < x ≤ 10, f(x) = 3x
Also, at x = 3, f(x) = 32 = 9 or f(x) = 3 × 3 = 9
i.e., at x = 3, f(x) = 9
Therefore, for 0 ≤ x ≤ 10, the images of f(x) are unique.
Thus, the given relation is a function.
The relation g is defined as
It can be observed that for x = 2, g(x) = 22 = 4 and g(x) = 3 × 2 = 6
Hence, element 2 of the domain of the relation g corresponds to two different images i.e., 4 and 6. Hence, this relation is not a function.
Page No 46:
Question 2:
If f(x) = x2, find.
ANSWER:
Page No 46:
Question 3:
Find the domain of the function
ANSWER:
The given function is.
It can be seen that function f is defined for all real numbers except at x = 6 and x = 2.
Hence, the domain of f is R – {2, 6}.
Page No 46:
Question 4:
Find the domain and the range of the real function f defined by.
ANSWER:
The given real function is.
It can be seen that is defined for (x – 1) ≥ 0.
i.e., is defined for x ≥ 1.
Therefore, the domain of f is the set of all real numbers greater than or equal to 1 i.e., the domain of f = [1,).
As x ≥ 1 ⇒ (x – 1) ≥ 0 ⇒
Therefore, the range of f is the set of all real numbers greater than or equal to 0 i.e., the range of f = [0,).
Page No 46:
Question 5:
Find the domain and the range of the real function f defined by f (x) = |x – 1|.
ANSWER:
The given real function is f (x) = |x – 1|.
It is clear that |x – 1| is defined for all real numbers.
∴Domain of f = R
Also, for x ∈ R, |x – 1| assumes all real numbers.
Hence, the range of f is the set of all non-negative real numbers.
Page No 46:
Question 6:
Let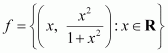
ANSWER:
The range of f is the set of all second elements. It can be observed that all these elements are greater than or equal to 0 but less than 1.
[Denominator is greater numerator]
Thus, range of f = [0, 1)
Page No 46:
Question 7:
Let f, g: R → R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and.
ANSWER:
f, g: R → R is defined as f(x) = x + 1, g(x) = 2x – 3
(f + g) (x) = f(x) + g(x) = (x + 1) + (2x – 3) = 3x – 2
∴(f + g) (x) = 3x – 2
(f – g) (x) = f(x) – g(x) = (x + 1) – (2x – 3) = x + 1 – 2x + 3 = – x + 4
∴ (f – g) (x) = –x + 4
Page No 46:
Question 8:
Let f = {(1, 1), (2, 3), (0, –1), (–1, –3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.
ANSWER:
f = {(1, 1), (2, 3), (0, –1), (–1, –3)}
f(x) = ax + b
(1, 1) ∈ f
⇒ f(1) = 1
⇒ a × 1 + b = 1
⇒ a + b = 1
(0, –1) ∈ f
⇒ f(0) = –1
⇒ a × 0 + b = –1
⇒ b = –1
On substituting b = –1 in a + b = 1, we obtain a + (–1) = 1 ⇒ a = 1 + 1 = 2.
Thus, the respective values of a and b are 2 and –1.
Page No 46:
Question 9:
Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b2}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
ANSWER:
R = {(a, b): a, b ∈ N and a = b2}
(i) It can be seen that 2 ∈ N;however, 2 ≠ 22 = 4.
Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is not true.
(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 32.
Now, 3 ≠ 92 = 81; therefore, (3, 9) ∉ N
Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R” is not true.
(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 42 and 4 = 22.
Now, 16 ≠ 22 = 4; therefore, (16, 2) ∉ N
Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.
Page No 46:
Question 10:
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Are the following true?
(i) f is a relation from A to B (ii) f is a function from A to B.
Justify your answer in each case.
ANSWER:
A = {1, 2, 3, 4} and B = {1, 5, 9, 11, 15, 16}
∴A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11), (3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
It is given that f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
(i) A relation from a non-empty set A to a non-empty set B is a subset of the Cartesian product A × B.
It is observed that f is a subset of A × B.
Thus, f is a relation from A to B.
(ii) Since the same first element i.e., 2 corresponds to two different images i.e., 9 and 11, relation f is not a function.
Page No 47:
Question 11:
Let f be the subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer.
ANSWER:
The relation f is defined as f = {(ab, a + b): a, b ∈ Z}
We know that a relation f from a set A to a set B is said to be a function if every element of set A has unique images in set B.
Since 2, 6, –2, –6 ∈ Z, (2 × 6, 2 + 6), (–2 × –6, –2 + (–6)) ∈ f
i.e., (12, 8), (12, –8) ∈ f
It can be seen that the same first element i.e., 12 corresponds to two different images i.e., 8 and –8. Thus, relation f is not a function.
Page No 47:
Question 12:
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
ANSWER:
A = {9, 10, 11, 12, 13}
f: A → N is defined as
f(n) = The highest prime factor of n
Prime factor of 9 = 3
Prime factors of 10 = 2, 5
Prime factor of 11 = 11
Prime factors of 12 = 2, 3
Prime factor of 13 = 13
∴f(9) = The highest prime factor of 9 = 3
f(10) = The highest prime factor of 10 = 5
f(11) = The highest prime factor of 11 = 11
f(12) = The highest prime factor of 12 = 3
f(13) = The highest prime factor of 13 = 13
The range of f is the set of all f(n), where n ∈ A.
∴Range of f = {3, 5, 11, 13}